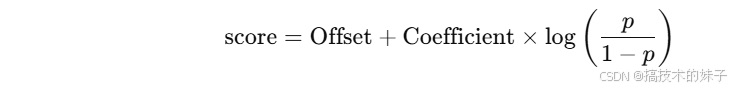
《银行信用评分卡模型训练全过程:数据处理、特征工程、特征选择、模型调优到模型的完美实践》-python
假设我们有一个银行信用评估数据集,包含了客户的基本信息以及历史信用记录等特征。年龄 (Age)年收入 (Annual Income)信用历史 (Credit History Length)负债比例 (Debt-to-Income Ratio)是否违约 (Default) - 目标变量,1 表示违约,0 表示未违约。
《银行信用评分卡模型全解析:从数据处理到模型部署,打造精准风控神器》
数据集概述
假设我们有一个银行信用评估数据集,包含了客户的基本信息以及历史信用记录等特征。数据集的结构如下:
年龄 (Age)
年收入 (Annual Income)
信用历史 (Credit History Length)
负债比例 (Debt-to-Income Ratio)
是否违约 (Default) - 目标变量,1 表示违约,0 表示未违约
代码结构
1. 导入依赖和加载数据
首先,我们导入必要的库并加载数据:
python
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_auc_score, accuracy_score, confusion_matrix
from scipy import stats
# 模拟一个银行信用评估的数据集
data = {
'年龄': [25, 34, 40, 50, 30, 28, 39, 43, 60, 45, 50, 30, 29, 40, 39],
'年收入': [30, 40, 25, 60, 45, 35, 50, 65, 70, 55, 45, 30, 40, 50, 65],
'信用历史': [5, 10, 15, 20, 8, 7, 10, 12, 18, 20, 19, 6, 7, 9, 12],
'负债比例': [0.3, 0.4, 0.2, 0.6, 0.5, 0.3, 0.2, 0.4, 0.3, 0.4, 0.5, 0.3, 0.4, 0.2, 0.6],
'是否违约': [0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 1, 1]
}
df = pd.DataFrame(data)
# 查看数据
print(df.head())
2. 卡方分箱 (Chi-Square Binning)
我们使用卡方分箱(Chi-Square Binning)来对数值型变量进行分箱。这里我们以“年龄”和“年收入”两个变量为例:
python
def chi_square_binning(df, feature, target, max_bins=5):
"""
使用卡方检验进行分箱
"""
df[feature] = pd.cut(df[feature], bins=max_bins, right=False)
binned_df = pd.crosstab(df[feature], df[target])
chi2, p, _, _ = stats.chi2_contingency(binned_df)
print(f"{feature}的卡方检验结果:Chi2 = {chi2}, P-value = {p}")
return df
df = chi_square_binning(df, '年龄', '是否违约')
df = chi_square_binning(df, '年收入', '是否违约')
print(df.head())
3. 特征工程 (Feature Engineering)
在这一步,我们会对数据进行一些特征处理,包括缺失值处理、标准化、编码和WOE(Weight of Evidence)转化。
python
# 处理缺失值(此处假设没有缺失值,但可以用df.fillna()来填充)
# 对分类变量进行独热编码
df_encoded = pd.get_dummies(df, drop_first=True)
# WOE转化:我们用一个简单的函数来对变量进行WOE转化
def calculate_woe(df, feature, target):
"""
计算WOE(Weight of Evidence)
"""
grouped = df.groupby(feature)[target].agg(['count', 'sum'])
grouped['non_event'] = grouped['count'] - grouped['sum']
grouped['event_rate'] = grouped['sum'] / grouped['sum'].sum()
grouped['non_event_rate'] = grouped['non_event'] / grouped['non_event'].sum()
grouped['WOE'] = np.log(grouped['event_rate'] / grouped['non_event_rate'])
# 将WOE值合并回原始数据
df = df.merge(grouped[['WOE']], left_on=feature, right_index=True, how='left')
return df
# 对每个特征应用WOE转换
df_encoded = calculate_woe(df_encoded, '年龄', '是否违约')
df_encoded = calculate_woe(df_encoded, '年收入', '是否违约')
print(df_encoded.head())
4. 变量筛选 (Variable Selection)
通过计算每个变量的信息值(IV),我们可以评估哪些变量对目标变量的预测能力最强。IV值越高,变量的重要性越高。
python
def calculate_iv(df, feature, target):
"""
计算变量的信息值(IV)
"""
grouped = df.groupby(feature)[target].agg(['count', 'sum'])
grouped['non_event'] = grouped['count'] - grouped['sum']
grouped['event_rate'] = grouped['sum'] / grouped['sum'].sum()
grouped['non_event_rate'] = grouped['non_event'] / grouped['non_event'].sum()
grouped['WOE'] = np.log(grouped['event_rate'] / grouped['non_event_rate'])
grouped['IV'] = (grouped['event_rate'] - grouped['non_event_rate']) * grouped['WOE']
iv = grouped['IV'].sum()
return iv
# 计算IV值
age_iv = calculate_iv(df_encoded, '年龄', '是否违约')
income_iv = calculate_iv(df_encoded, '年收入', '是否违约')
print(f"年龄的IV值: {age_iv}")
print(f"年收入的IV值: {income_iv}")
5. 模型训练 (Model Training)
在特征工程和变量筛选之后,我们将数据集拆分为训练集和测试集,并训练一个逻辑回归模型。
python
# 数据拆分
X = df_encoded[['年龄WOE', '年收入WOE', '信用历史', '负债比例']]
y = df_encoded['是否违约']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 训练逻辑回归模型
model = LogisticRegression()
model.fit(X_train, y_train)
# 模型评估
y_pred = model.predict(X_test)
y_pred_proba = model.predict_proba(X_test)[:, 1]
# 评估模型性能
accuracy = accuracy_score(y_test, y_pred)
roc_auc = roc_auc_score(y_test, y_pred_proba)
print(f"模型准确率: {accuracy:.2f}")
print(f"ROC AUC: {roc_auc:.2f}")
6. 模型调参 (Model Tuning)
为了优化模型性能,我们可以调整逻辑回归模型的超参数,如正则化强度(C值):
python
from sklearn.model_selection import GridSearchCV
# 调参:使用GridSearchCV优化C值
param_grid = {'C': [0.1, 1, 10, 100]}
grid_search = GridSearchCV(LogisticRegression(), param_grid, cv=5, scoring='roc_auc')
grid_search.fit(X_train, y_train)
# 输出最佳参数和得分
print("最佳参数:", grid_search.best_params_)
print("最佳ROC AUC:", grid_search.best_score_)
# 用最佳参数训练模型
best_model = grid_search.best_estimator_
y_pred_best = best_model.predict(X_test)
y_pred_proba_best = best_model.predict_proba(X_test)[:, 1]
# 评估调参后的模型
accuracy_best = accuracy_score(y_test, y_pred_best)
roc_auc_best = roc_auc_score(y_test, y_pred_proba_best)
print(f"调参后的模型准确率: {accuracy_best:.2f}")
print(f"调参后的ROC AUC: {roc_auc_best:.2f}")
- 模型评估 (Model Evaluation)
通过混淆矩阵、准确率、AUC等指标,进一步评估模型的表现:
python
# 混淆矩阵
conf_matrix = confusion_matrix(y_test, y_pred_best)
print("混淆矩阵:")
print(conf_matrix)
# 绘制ROC曲线
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve
fpr, tpr, _ = roc_curve(y_test, y_pred_proba_best)
plt.plot(fpr, tpr, color='blue', label='ROC curve')
plt.plot([0, 1], [0, 1], color='gray', linestyle='--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate
``
## 8. 特征交互与多项式特征
在实际的评分卡模型中,除了对单个特征进行处理外,还可以考虑特征之间的交互作用。例如,某些变量组合可能比单独的特征更能有效预测违约概率。通过特征交互或多项式特征,可以进一步提高模型的表现。
示例:特征交互和多项式特征
python
```python
from sklearn.preprocessing import PolynomialFeatures
# 使用多项式特征,生成交互特征
poly = PolynomialFeatures(degree=2, interaction_only=True)
X_poly = poly.fit_transform(X)
# 将生成的交互特征加入到模型中
X_poly_df = pd.DataFrame(X_poly, columns=poly.get_feature_names(X.columns))
# 查看生成的交互特征
print(X_poly_df.head())
在上面的代码中,我们使用PolynomialFeatures来生成特征的交互项和多项式特征。通过这种方式,我们能够捕捉到变量之间更复杂的关系,在某些情况下,交互特征可能会显著提升模型性能。
9. 模型集成
评分卡模型可以通过模型集成的方法进一步提升表现。集成方法比如 随机森林 和 梯度提升树(GBDT),可以处理非线性关系和特征间的复杂交互,并且通常会比单一的逻辑回归模型表现更好。
示例:随机森林模型
python
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report
# 训练随机森林模型
rf_model = RandomForestClassifier(n_estimators=100, random_state=42)
rf_model.fit(X_train, y_train)
# 预测
y_pred_rf = rf_model.predict(X_test)
# 评估
accuracy_rf = accuracy_score(y_test, y_pred_rf)
roc_auc_rf = roc_auc_score(y_test, rf_model.predict_proba(X_test)[:, 1])
print(f"随机森林模型准确率: {accuracy_rf:.2f}")
print(f"随机森林模型ROC AUC: {roc_auc_rf:.2f}")
# 打印分类报告
print("分类报告:")
print(classification_report(y_test, y_pred_rf))
通过使用随机森林或其他集成方法(如 XGBoost 或 LightGBM),我们可以获得更好的性能,尤其是在数据中包含复杂的非线性关系时。
10. 模型稳定性和解释性
在银行信用评估中,模型的稳定性和解释性非常重要。银行需要能够理解评分卡模型背后的决策逻辑。因此,除了准确性之外,还需要对模型的可解释性进行优化。逻辑回归模型本身具有很好的可解释性,但如果使用了更复杂的模型(如随机森林或XGBoost),我们可以使用 SHAP(Shapley Additive Explanations) 或 LIME(Local Interpretable Model-agnostic Explanations) 来解释模型的预测。
示例:使用SHAP解释模型
python
import shap
# 使用SHAP解释随机森林模型
explainer = shap.TreeExplainer(rf_model)
shap_values = explainer.shap_values(X_test)
# 绘制SHAP值的图形
shap.summary_plot(shap_values[1], X_test) # 1代表预测为1的类别
SHAP值帮助我们了解每个特征在模型预测中的贡献,以及模型如何利用这些特征做出决策。通过这种方式,银行能够了解哪些特征在信用评估中最为关键。
11. 评分卡的标准化与转换
评分卡模型最终会输出一个分数,用于表示客户的信用风险。为了使分数具有实际意义,我们需要将预测结果映射为信用分数。
一般来说,评分卡模型通过以下步骤将预测概率转化为信用分数:
计算模型预测的概率:通常使用逻辑回归模型来预测客户违约的概率。
通过线性转换公式计算分数:例如,假设一个标准分数卡的最大分数为 1000 分,可以通过如下公式将概率转化为分数:

其中,p 是模型的预测概率。
示例:评分卡转换
python
def calculate_score(probability, offset=600, coefficient=20):
"""
通过预测概率计算信用评分
"""
score = offset + coefficient * np.log(probability / (1 - probability))
return score
# 获取测试集的预测概率
probabilities = rf_model.predict_proba(X_test)[:, 1]
# 计算每个客户的信用分数
scores = [calculate_score(prob) for prob in probabilities]
# 查看前几个客户的信用分数
print(scores[:10])
在上面的代码中,calculate_score函数将逻辑回归的预测概率转换为信用评分。通过调整offset和coefficient,我们可以对评分卡进行定制,以满足不同银行或金融机构的需求。
12. 模型的部署和实时预测
在信用评分模型完成训练和调优后,下一步通常是将模型部署到生产环境中,并实现实时预测。部署模型的方式可能包括:
将模型保存为Pickle或Joblib格式,并在服务器上加载进行预测。
将模型作为REST API接口提供服务,接受请求并返回预测结果。
示例:模型保存和加载
python
import joblib
# 保存模型
joblib.dump(rf_model, 'credit_scoring_model.pkl')
# 加载模型
loaded_model = joblib.load('credit_scoring_model.pkl')
# 使用加载的模型进行预测
loaded_model.predict(X_test)
通过这种方式,银行或金融机构可以将训练好的模型部署到生产环境,实现实时的信用评分功能。
13. 模型的监控与维护
随着时间的推移,数据分布可能会发生变化,模型的性能可能会逐渐下降。因此,模型的监控和维护变得非常重要。为了确保模型的长期有效性,我们需要定期评估模型的性能,并在必要时进行重新训练。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容






所有评论(0)