✅博主简介：本人擅长数据处理、建模仿真、程序设计、论文写作与指导，项目与课题经验交流。项目合作可私信或扫描文章底部二维码。

---

无人机路径规划中，首先需要根据无人机的飞行特性以及飞行环境建立路径规划模型。该模型主要包括三个关键部分：飞行环境、性能约束和路径规划评价指标。

1. 飞行环境建模： 无人机飞行环境主要由地形、障碍物、建筑物以及飞行禁区等组成。对于复杂的城市环境来说，地面建筑物、山地等障碍物会对无人机的路径规划产生较大影响。无人机路径规划的核心目标是生成一条避免这些障碍物的飞行路线。飞行环境通常用网格模型或者三维地形模型来描述，网格模型通过离散化的方式将环境划分为若干小网格，便于路径规划算法进行搜索和路径生成。

2. 性能约束： 无人机在飞行过程中会受到动力学限制，如最大飞行速度、最小转弯半径、最大航程以及飞行高度约束等。例如，最小转弯半径限制了无人机在转弯时的急剧变化，避免路径规划中出现不合理的急转弯。同时，无人机的航程约束决定了其路径长度不能超出电池的供电范围。

3. 路径规划评价指标：

   • 路径长度代价：路径长度直接决定了无人机的飞行时间和任务完成效率，因此路径长度越短越好。
   • 油耗代价：无人机的电池续航能力有限，规划路径时需要考虑最小化油耗代价。
   • 障碍物威胁代价：无人机在飞行过程中应尽量远离障碍物，因此需要考虑障碍物的威胁代价，以避免碰撞。
   • 飞行高度代价：飞行高度会影响无人机的能耗和飞行安全性，通常需要保持在规定的高度范围内。

变权重A*算法的提出与优化

A算法是常用的路径规划算法之一，基于启发式搜索原则，通过估算起点到终点的代价来指导路径的生成。然而，在无人机路径规划中，传统A算法可能出现冗余节点过多、搜索效率较慢、路径不平滑等问题。为了解决这些问题，提出了变权重A*算法。

1. 变权重策略： 传统A算法的启发式函数是静态的，即在搜索过程中所有节点的启发值均相同。变权重A算法通过根据无人机的当前位置动态调整启发式函数与代价函数的权重。例如，当无人机接近障碍物时，启发式权重可以适当提高，以增加对障碍物的规避能力；而当无人机距离目标点较近时，则可以降低启发式权重，以加快搜索速度。这个动态权重机制有效提升了算法的搜索效率，并减少了冗余节点的生成。

2. 路径平滑化： 为了进一步提高路径的可用性和飞行的平滑性，采用了B样条算法对变权重A算法生成的路径进行二次优化。B样条法通过插值计算出平滑的路径，消除了因A算法产生的冗余节点和急转弯，使无人机可以顺畅地沿着平滑路径飞行。

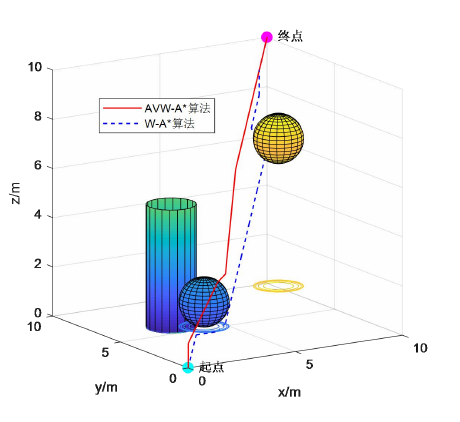
3. 仿真验证： 在三维仿真环境中，通过对比A算法和变权重A算法，变权重A算法的搜索时间较A算法缩短了74.10%，路径长度缩短了12.39%。这证明了变权重A*算法的高效性和可行性，尤其适合在无人机飞行环境复杂的场景中应用。

改进的A势场算法（A-APF）

在传统的路径规划算法中，人工势场算法（APF）因其计算效率高、实时性好而受到广泛应用，但该算法容易陷入局部最优解的问题，导致无人机可能无法顺利避开障碍物。因此，提出了A势场算法（A-APF），该算法将A*算法与人工势场算法相结合，利用两者的优点实现更为智能的路径规划。

1. A-APF算法的核心思想*： 无人机首先基于改进的A算法生成初始路径，当飞行过程中接近障碍物时，切换到APF算法以避开障碍物。当无人机逃离障碍物的势力范围后，重新沿着A算法规划的原始路径飞行。通过这种方式，克服了传统APF算法局部最优的问题，并确保了全局路径的最优性。

2. 动态环境下的避障能力： 在动态障碍物环境下，A*-APF算法通过实时调整势场函数，使无人机在遇到动态障碍物时能够快速响应并规划出安全的飞行路径。仿真结果显示，改进的APF算法相比传统APF算法，路径长度减少了4.32%，规划时间减少了25.00%，迭代次数减少了20.35%，证明了该算法在动态环境下的有效性。

虚拟天牛须搜索算法（VBAS）

针对传统的天牛须搜索算法（Beetle Antennae Search, BAS）容易陷入局部最优解的问题，并且生成路径可能会产生路径震荡，提出了虚拟天牛须搜索算法（Virtual Beetle Antennae Search, VBAS），该算法在无人机路径规划中表现出了更好的性能。

1. 虚拟目标点生成： 在VBAS算法中，当无人机即将接触到障碍物时，会生成一个虚拟目标点，引导无人机绕过障碍物。该虚拟目标点的生成基于无人机与障碍物之间的相对位置，通过预测障碍物的威胁程度来调整虚拟目标点的坐标位置。这样无人机可以顺利避开障碍物，并继续向目标点飞行。

2. 路径震荡的消除： 在路径规划过程中，VBAS算法会对每一段路径进行震荡检测，如果某段路径出现了较大的波动或者震荡，则会对该路径进行修剪，以确保路径的平滑性和安全性。经过多次迭代后，VBAS算法生成的路径不仅避开了障碍物，还具有较高的平滑度，适合无人机稳定飞行。

3. 路径优化： 当VBAS算法生成了全部路径集后，利用B样条法对路径进行二次优化，确保最终生成的路径平滑且无碰撞。通过在不同环境下的仿真实验，VBAS算法展现了其在复杂场景中的优越性。无论是在静态还是动态障碍物环境下，VBAS算法都能够有效提升无人机的路径规划能力。

4. 仿真结果分析： 仿真实验表明，VBAS算法不仅能够避免局部最优解问题，还可以消除路径震荡现象，使得无人机能够在复杂环境中生成稳定的飞行路径。相比于传统BAS算法，VBAS算法在路径规划时间上减少了约30.15%，路径平滑性得到了显著提升。此外，VBAS算法在障碍物密集的环境下表现出更强的避障能力和鲁棒性。

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import splprep, splev

# 搜索节点
class Node:
    def __init__(self, position=None, parent=None):
        self.position = position
        self.parent = parent
        self.g = 0
        self.h = 0
        self.f = 0

def astar(maze, start, end):
    start_node = Node(start, None)
    end_node = Node(end, None)
    open_list = []
    closed_list = []
    open_list.append(start_node)

    while open_list:
        current_node = open_list[0]
        current_index = 0
        for index, item in enumerate(open_list):
            if item.f < current_node.f:
                current_node = item
                current_index = index

        open_list.pop(current_index)
        closed_list.append(current_node)

        if current_node.position == end_node.position:
            path = []
            current = current_node
            while current is not None:
                path.append(current.position)
                current = current.parent
            return path[::-1]

        children = []
        for new_position in [(0, -1), (0, 1), (-1, 0), (1, 0), (-1, -1), (-1, 1), (1, -1), (1, 1)]:
            node_position = (current_node.position[0] + new_position[0], current_node.position[1] + new_position[1])
            if node_position[0] > (len(maze) - 1) or node_position[0] < 0 or node_position[1] > (len(maze[len(maze)-1]) -