智能优化系列|第一期:自适应大领域搜索算法(ALNS算法)详解与实战案例(附python代码)
Adaptive Large Neighborhood Search (ALNS) 算法是一种元启发式算法,用于解决组合优化问题。ALNS 算法结合了离散优化中的邻域搜索和元启发式算法的特点,能够有效地应对各种复杂的优化问题。ALNS 算法的核心思想自适应大领域搜索的核心思想是:破坏解、修复解、动态调整权重并选择(自适应)。通过设计多组破坏算子和修复算子,扩大解空间搜索范围,对当前解进行改进,表
1.ALNS 算法核心思想
Adaptive Large Neighborhood Search (ALNS) 算法是一种元启发式算法,用于解决组合优化问题。ALNS 算法结合了离散优化中的邻域搜索和元启发式算法的特点,能够有效地应对各种复杂的优化问题。
ALNS 算法的核心思想自适应大领域搜索的核心思想是:破坏解、修复解、动态调整权重并选择(自适应)。通过设计多组破坏算子和修复算子,扩大解空间搜索范围,对当前解进行改进,表现好的破坏和修复方法相应地得到高分,权重也越高。在每次迭代中,根据以往表现对各个破坏和修复算子进行选择和权重调整,使用高效的组合方法,提高算法寻优能力,从而找到最优解。
破坏算子(destroy)
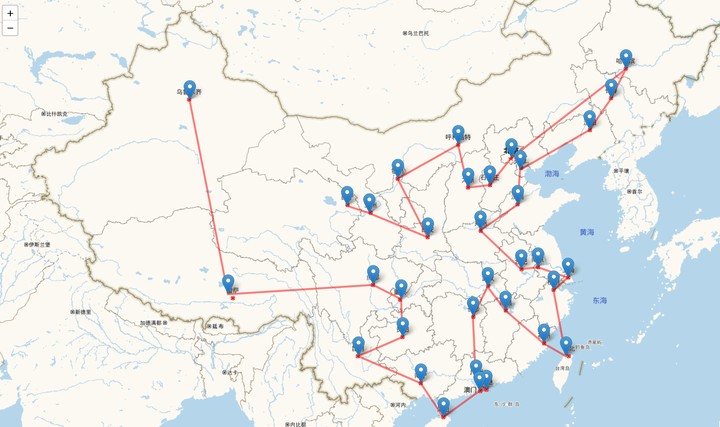
破坏算子在ALNS中用于破坏当前解,并生成新的候选解。常见的破坏算子包括随机移除、最差移除、相似移除等。针对destroy算子,首先需要确定的是destroy的比例,例如下面将介绍的34个城市的TSP问题,如果destroy比例为10%,则需要删除3个城市;然后还要确定删除哪3个,这就有 C(34,3)= 5984种情况
修复算子(repair)
修复算子是指在求解过程中用于修复产生的不可行解的一种策略,以便继续搜索更优的解。修复算子跟破坏算子是成对出现的,先破坏解(destroy)然后修复解(repair)。常见的修复算子包括随机插入、贪婪插入等。其中,随机插入将移除的节点逐个插入到破坏后解的任意位置;贪婪插入将移除的节点插到距离成本最小,即插入后总路径最短的位置中。
动态调整权重并选择算子
(1)权重更新

算子的权重按这个公式进行更新:
式中,Wd为算子权重,Sd为算子分数,Ud为算子的使用次数,ρ为权重更新系数(控制权重变化的速度)。其实就是:算子新权重 = 算子旧权重 × (1 - 系数) + 系数 × (累加分数 ÷ 累加次数),将算子权重与以往表现挂钩。
在开始时,所有算子均具有相同的权重和分值。而分数,则是在每个迭代过程中,根据算子的不同表现情况阶梯式给分,得分越高表明算子表现越好。可设定以下4种加分情况:
(1)破坏/修复后得到新的全局最优解,+1.5分
(2)破坏/修复后没有得到全局最优解:
①尚未接受过的但比当前解好,+1.2分
②尚未接受过的且比当前解差:
a)在一定标准下接受劣解,+0.8分
b)不满足接受准则的劣解,+0.6分
阶梯分数自己定,1.5、1.2为示例。搜索过程中,若只接受优解容易陷入局部最优,为了避免这种情况应采用一定准则接受劣解。自适应大领域搜索中通常采用模拟退火算法Metropolis准则,在一定概率下接受劣解。
(2)选择算子
得到新的权重后,算法基于轮盘赌的思想对算子进行选择,即算子的概率越大,被选中的概率越大。
2.ALNS算法的伪代码
下图是ALNS的伪代码:


3.ALNS算法实现34个城市的TSP问题
以下是python实现的代码。 其中,destroy算子有3个:随机筛选N个城市、删除距离最大的N个城市和随机删除连续的N个城市;repair算子有2个:随机插入和贪心插入,不过考虑到随机插入的效果大概率比较差,所以代码中实际只使用了贪心插入。
核心算子的代码如下:
@staticmethod
def dis_cal(path, dist_mat):
distance = 0
for i in range(len(path) - 1):
distance += dist_mat[path[i]][path[i + 1]]
distance += dist_mat[path[-1]][path[0]]
return distance
# 随机删除N个城市
@staticmethod
def random_destroy(x, destroy_city_cnt):
new_x = copy.deepcopy(x)
removed_cities = []
# 随机选择N个城市,并删除
removed_index = random.sample(range(0, len(x)), destroy_city_cnt)
for i in removed_index:
removed_cities.append(new_x[i])
x.remove(new_x[i])
return removed_cities
# 删除距离最大的N个城市
@staticmethod
def max_n_destroy(x, destroy_city_cnt):
new_x = copy.deepcopy(x)
removed_cities = []
# 计算顺序距离并排序
dis = []
for i in range(len(new_x) - 1):
dis.append(dist_mat[new_x[i]][new_x[i + 1]])
dis.append(dist_mat[new_x[-1]][new_x[0]])
sorted_index = np.argsort(np.array(dis))
# 删除最大的N个城市
for i in range(destroy_city_cnt):
removed_cities.append(new_x[sorted_index[-1 - i]])
x.remove(new_x[sorted_index[-1 - i]])
return removed_cities
# 随机删除连续的N个城市
@staticmethod
def continue_n_destroy(x, destroy_city_cnt):
new_x = copy.deepcopy(x)
removed_cities = []
# 随机选择N个城市,并删除
removed_index = random.sample(range(0, len(x) - destroy_city_cnt), 1)[0]
for i in range(removed_index + destroy_city_cnt, removed_index, -1):
removed_cities.append(new_x[i])
x.remove(new_x[i])
return removed_cities
# destroy操作
def destroy(self, flag, x, destroy_city_cnt):
# 三个destroy算子,第一个是随机删除N个城市,第二个是删除距离最大的N个城市,第三个是随机删除连续的N个城市
removed_cities = []
if flag == 0:
# 随机删除N个城市
removed_cities = self.random_destroy(x, destroy_city_cnt)
elif flag == 1:
# 删除距离最大的N个城市
removed_cities = self.max_n_destroy(x, destroy_city_cnt)
elif flag == 2:
# 随机删除连续的N个城市
removed_cities = self.continue_n_destroy(x, destroy_city_cnt)
return removed_cities
# 随机插入
def random_insert(x, removed_cities):
insert_index = random.sample(range(0, len(x)), len(removed_cities))
for i in range(len(insert_index)):
x.insert(insert_index[i], removed_cities[i])
# 贪心插入
def greedy_insert(self, x, removed_cities):
dis = float('inf')
insert_index = -1
for i in range(len(removed_cities)):
# 寻找插入后的最小总距离
for j in range(len(x) + 1):
new_x = copy.deepcopy(x)
new_x.insert(j, removed_cities[i])
if self.dis_cal(new_x, dist_mat) < dis:
dis = self.dis_cal(new_x, dist_mat)
insert_index = j
# 最小位置处插入
x.insert(insert_index, removed_cities[i])
dis = float('inf')
# repair操作
def repair(self, flag, x, removed_cities):
# 两个repair算子,第一个是随机插入,第二个贪心插入
if flag == 0:
self.random_insert(x, removed_cities)
elif flag == 1:
self.greedy_insert(x, removed_cities)
# 选择destroy算子
def select_and_destroy(self, destroy_w, x, destroy_city_cnt):
# 轮盘赌逻辑选择算子
prob = destroy_w / np.array(destroy_w).sum()
seq = [i for i in range(len(destroy_w))]
destroy_operator = np.random.choice(seq, size=1, p=prob)[0]
# destroy操作
removed_cities = self.destroy(destroy_operator, x, destroy_city_cnt)
return removed_cities, destroy_operator
# 选择repair算子
def select_and_repair(self, repair_w, x, removed_cities):
# # 轮盘赌逻辑选择算子
prob = repair_w / np.array(repair_w).sum()
seq = [i for i in range(len(repair_w))]
repair_operator = np.random.choice(seq, size=1, p=prob)[0]
# repair操作:此处设定repair_operator=1,即只使用贪心策略
self.repair(1, x, removed_cities)
return repair_operator运行代码后可发现,经过不到4s的计算时间,ALNS便可以得到15662.59的解,和全局最优解15614.84之间的gap仅约0.3%。
4.结果绘图

相关视频会在后续发布,欢迎关注我的bilibili:无形忍者的个人空间-无形忍者个人主页-哔哩哔哩视频
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容








所有评论(0)