机器学习05-聚类算法（python）SC（轮廓系数）详解

凝聚度表示与簇 1 中其他点的平均距离。分离度表示) 与最近簇（簇 2）的平均距离。轮廓系数，表示样本聚类效果较好，值接近 1，说明它更好地属于它所在的簇。

weixin_41645791

1596人浏览 · 2024-09-14 21:20:48

weixin_41645791 · 2024-09-14 21:20:48 发布

$S = \frac{(b - a)}{\max(a, b)}$

# 导入必要的库
from sklearn.cluster import KMeans  # 导入 KMeans 聚类算法
import matplotlib.pyplot as plt  # 导入 matplotlib 用于绘图
from sklearn.datasets import make_blobs  # 导入 make_blobs 用于生成模拟数据
from sklearn.metrics import silhouette_score  # 导入 silhouette_score 用于计算轮廓系数

# 定义函数来计算不同簇数下的轮廓系数
def dm02_silhouette_coefficient():
    silhouette_list = []  # 初始化一个空列表，用于存储每个簇数下的轮廓系数

    # 生成模拟数据集
    # n_samples=1000 生成1000个样本
    # n_features=2 表示每个样本有2个特征（二维数据）
    # centers 指定了4个聚类中心，分别为 [-1, -1], [0, 0], [1, 1], [2, 2]
    # cluster_std 指定每个聚类的标准差，数值越小簇内点越集中
    x, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1, -1], [0, 0], [1, 1], [2, 2]],
                      cluster_std=[0.4, 0.2, 0.2, 0.2], random_state=22)  # 固定随机种子使每次生成的数据一致

    # 计算不同簇数下的轮廓系数
    for clu_num in range(2, 100):  # 从2个簇开始，计算到99个簇
        # 初始化 KMeans 模型，指定簇数和最大迭代次数
        my_kmeans = KMeans(n_clusters=clu_num, max_iter=100, random_state=0)
        # 拟合模型，对数据进行聚类
        my_kmeans.fit(x)
        # 预测簇标签
        cluster_labels = my_kmeans.predict(x)
        # 计算轮廓系数并添加到列表中，轮廓系数衡量了聚类结果的优劣
        silhouette_list.append(silhouette_score(x, cluster_labels))

    # 绘制轮廓系数随簇数变化的图
    plt.figure(figsize=(18, 8), dpi=100)  # 设置图像大小和分辨率
    plt.xticks(range(0, 100, 3), labels=range(0, 100, 3))  # 设置 x 轴刻度
    plt.grid(True)  # 显示网格线
    plt.title('Silhouette Coefficient vs. Number of Clusters')  # 设置图像标题
    plt.xlabel('Number of Clusters')  # 设置 x 轴标签
    plt.ylabel('Silhouette Coefficient')  # 设置 y 轴标签
    # 绘制簇数与轮廓系数的曲线，'ob-' 表示蓝色圆圈连接线
    plt.plot(range(2, 100), silhouette_list, 'ob-', markersize=5, label='Silhouette Coefficient')
    plt.legend(loc='best')  # 显示图例
    plt.show()  # 显示图像

    # 通过观察图像，可以找到轮廓系数达到最大值的位置，该位置通常是最优的簇数

# 调用函数进行计算并绘图
dm02_silhouette_coefficient()

数据集示例

计算公式：

$SC_i = \frac{b_i - a_i}{\max(a_i, b_i)}$

为了更清晰地解释如何计算每个样本的分离度 $a_i$ 和轮廓系数 $b_i$ ，以及轮廓系数SC我们通过一个例子来详细说明。

例子：计算样本的分离度和轮廓系数

假设我们有以下三个簇的二维数据点：
- 簇 1： $( P_1(1, 2), P_2(2, 3), P_3(3, 2) )$
- 簇 2： $( P_4(6, 8), P_5(7, 8), P_6(8, 9) )$
- 簇 3： $( P_7(10, 1), P_8(9, 2), P_9(11, 2) )$
我们要计算样本 $P_1(1, 2)$ 的凝聚度、分离度和轮廓系数，并说明整个计算过程（注意本次只计算一个点的值，其他点计算凝聚度、分离度和轮廓系数是一样过程，最好计算SC 的时候，求了所有点的平均值轮廓系数SC ）。

第一步：计算凝聚度 ( $a_i$ )

凝聚度 ( $a_i$ ) 是样本 (i) 到所属簇中所有其他样本的平均距离。
- ( $P_1$ ) 属于簇 1，簇 1 中的其他样本是 $P_2(2, 3)$ 和 $P_3(3, 2)$ 。
- 计算 ( $P_1$ ) 到簇内其他样本的距离：
  - 到 $P_2(2, 3)$ 的距离： $\sqrt{(2 - 1)^2 + (3 - 2)^2} = \sqrt{1 + 1} = \sqrt{2} \approx 1.41$
  - 到 $P_3(3, 2)$ 的距离： $\sqrt{(3 - 1)^2 + (2 - 2)^2} = \sqrt{4 + 0} = \sqrt{4} = 2$
凝聚度 ( $a_1$ )： $a_1 = \frac{1.41 + 2}{2} = 1.71$

第二步：计算分离度 ( $b_i$ )

分离度 ( $b_i$ ) 是样本 (i) 到最近的其他簇的平均距离。
- ( $P_1$ ) 的最近簇是簇 2和簇 3，我们需要分别计算它到这两个簇的平均距离，然后选择距离最小的那个簇。
计算 (P_1) 到簇 2 的距离：
- 到 $P_4(6, 8)$ ： $\sqrt{(6 - 1)^2 + (8 - 2)^2} = \sqrt{25 + 36} = \sqrt{61} \approx 7.81$
- 到 $P_5(7, 8)$ ： $\sqrt{(7 - 1)^2 + (8 - 2)^2} = \sqrt{36 + 36} = \sqrt{72} \approx 8.49$
- 到 $P_6(8, 9)$ ： $\sqrt{(8 - 1)^2 + (9 - 2)^2} = \sqrt{49 + 49} = \sqrt{98} \approx 9.90$
簇 2 的平均距离： $b_1^{(2)} = \frac{7.81 + 8.49 + 9.90}{3} = \frac{26.2}{3} \approx 8.73$

计算 $P_1$ 到簇 3 的距离：
- 到 $P_7(10, 1)$ ： $\sqrt{(10 - 1)^2 + (1 - 2)^2} = \sqrt{81 + 1} = \sqrt{82} \approx 9.06$
- 到 $P_8(9, 2)$ ： $\sqrt{(9 - 1)^2 + (2 - 2)^2} = \sqrt{64} = 8$
- 到 $P_9(11, 2)$ ： $\sqrt{(11 - 1)^2 + (2 - 2)^2} = \sqrt{100} = 10$
簇 3 的平均距离： $[ b_1^{(3)} = \frac{9.06 + 8 + 10}{3} = \frac{27.06}{3} \approx 9.02 ]$

选择最近的簇：

分离度 $(b_1)$ 为 $(b_1 = \min(b_1^{(2)}, b_1^{(3)}) = \min(8.73, 9.02) = 8.73)$ ，因此簇 2是 $(P_1)$ 最近的簇。
即 $P_1$ 点的分离度 $(b_1)$ 为 8.73

第三步：计算轮廓系数 $(SC_i)$

轮廓系数 $(SC_i)$ 的公式是： $[ SC_i = \frac{b_i - a_i}{\max(a_i, b_i)} ]$

对于 $(P_1)$ 来说：
- 凝聚度 $(a_1 = 1.71)$
- 分离度 $(b_1 = 8.73)$
代入公式： $[ SC_1 = \frac{8.73 - 1.71}{\max(1.71, 8.73)} = \frac{7.02}{8.73} \approx 0.80 ]$

总结：
- 凝聚度 $(a_1 = 1.71)$ 表示 $(P_1)$ 与簇 1 中其他点的平均距离。
- 分离度 $(b_1 = 8.73)$ 表示 $(P_1$ ) 与最近簇（簇 2）的平均距离。
- 轮廓系数 $(SC_1 = 0.80)$ ，表示样本 $(P_1)$ 聚类效果较好，值接近 1，说明它更好地属于它所在的簇。
整体聚类模型的轮廓系数：

对所有样本的轮廓系数 $(SC_i)$ 计算后取平均，就可以得出聚类模型的整体轮廓系数，用来衡量聚类效果。

轮廓系数（Silhouette Coefficient，SC）的取值范围是 ([-1, 1])，这是因为它通过比较样本的凝聚度和分离度来衡量聚类效果。我们可以通过公式和直观解释来理解为什么它的取值范围是 $([-1, 1])$

轮廓系数的公式

轮廓系数 ( $SC_i$ ) 的计算公式为： $[ SC_i = \frac{b_i - a_i}{\max(a_i, b_i)} ]$ 其中：

$(a_i)$ 是样本 (i) 的凝聚度，即样本与其所属簇内其他样本的平均距离。
$(b_i)$ 是样本 (i) 的分离度，即样本与最近的其他簇的平均距离。

公式中的 $(SC_i)$ 用来衡量样本 (i) 是更接近它的自身簇，还是更接近最近的其他簇。

为什么取值在 ([-1, 1]) 之间？

当 $(SC_i = 1)$ 时：此时 $(a_i)$ 很小（样本与其所在簇内其他样本非常接近），而 $(b_i)$ 很大（样本与最近的其他簇的平均距离很远）。这是理想的情况，说明样本点与自己的簇高度匹配，并且远离其他簇，聚类效果非常好。
当 ( $SC_i = 0$ ) 时：此时 $(a_i$ ) 和 ( $b_i$ ) 相等，意味着样本点与它所在簇的其他点的距离和它与最近的其他簇的距离差不多。这表示样本点位于簇的边界，聚类效果不明显。
当 ( $SC_i = -1$ ) 时：此时 $(a_i > b_i)$ ，意味着样本点与其他簇的距离比与自己簇的距离更近，说明样本可能被错误地分配到了当前簇。这是最糟糕的情况，表示样本应该属于另一个簇。

取值范围的直观解释

当 ( $SC_i = 1$ )，说明样本与自己簇的其他样本非常接近，与其他簇的样本距离较远，表明聚类效果很好。
当 ( $SC_i = 0$ )，说明样本位于簇的边界，聚类效果中等，样本点无法明显区分到底更应该属于哪个簇。
当 ( $SC_i = -1$ )，说明样本距离其他簇的样本比自己簇的样本还要近，表明聚类效果很差，样本可能被错误归类。

因此，轮廓系数的范围 ([-1, 1]) 可以很好地反映聚类效果的好坏，从非常差（接近 -1）到非常好（接近 1）。

下面是描述过程，不过我理解上面应该很好的描述了计算过程：
计算凝聚度 ( $a_i$ ) 的流程如下：

凝聚度 (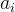 $a_i$ ) 是什么？

凝聚度 ( $a_i$ ) 是样本 (i) 与其所属簇内其他所有样本的平均距离。它反映了样本 (i) 在其所属簇内的紧密程度。凝聚度越小，表示样本与同一簇内其他样本越接近，簇内的聚类效果越好。

计算凝聚度 (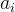 $a_i$ ) 的步骤：

找到样本 ( $P_i$ ) 所属的簇：首先确定样本 ( $P_i$ ) 所属的簇（即由聚类算法划分出的簇）。
计算样本 ( $P_i$ ) 到同一簇内其他样本的距离：
- 记 ( $C_k$ ) 为样本 ( $P_i$ ) 所在的簇（簇 (k)），该簇包含 ( $N_k$ ) 个样本。
- 对于 ( $P_i$ ) 所属的簇 ( $C_k$ )，计算 ( $P_i$ ) 到该簇内每个其他样本的距离。这些距离是欧氏距离（或者根据情况使用其他距离度量）。
求出簇内样本的平均距离：
- 将所有的距离求和，并除以簇内样本的总数减去 1（因为不包含样本自身）。公式如下：
$[ a_i = \frac{1}{N_k - 1} \sum_{P_j \in C_k, j \neq i} d(P_i, P_j) ]$

其中，( $d(P_i, P_j)$ ) 表示样本 ( $P_i$ ) 与样本 ( $P_j$ ) 之间的距离，( $N_k$ ) 是簇 ( $C_k$ ) 中的样本总数。

示例：

假设我们有一个样本 ( $P_1$ ) 位于簇 ( $C_k$ ) 中，而 ( $C_k$ ) 由 4 个样本 ( $P_1, P_2, P_3, P_4$ ) 组成。我们要计算样本 ( $P_1$ ) 的凝聚度 ( $a_1$ )。

计算 ( $P_1$ ) 到 ( $P_2$ )、( $P_1$ ) 到 ( $P_3$ )、( $P_1$ ) 到 ( $P_4$ ) 的距离。
将这些距离相加，并除以簇内的样本总数减 1（即 (3)）：

$[ a_1 = \frac{d(P_1, P_2) + d(P_1, P_3) + d(P_1, P_4)}{3} ]$
上面就得到了 $P_1$ 点的凝聚度 ( $a_1$ )（划重点，是P1点的，不是整个模型的）