离散数学 | 数理逻辑
介绍离散数学数理逻辑相关知识
目录
逻辑：研究人的思维的科学
思维过程： 概念-->判断-->推理
推理方法：
- 类比推理：由个别事实推出个别结论
- 归纳推理：由若干个别事实推出一般结论
- 演绎推理：由一般规律、个别事实推出个别结论
命题逻辑
命题
概念：命题是一个非真即假的陈述句
命题为真：所作的判断与客观一致，记做T（True）
命题为假：所作的判断与客观不一致，记做F（False）
注意：
1.感叹句、祈使句、疑问句不是命题
2.未知结果的命题为命题，但无法判断真假
3.悖论都不是命题
原子命题：由最简单的陈述句构成的命题
复合命题：由若干个原子命题构成的命题
联结词与复合命题
复合命题的构成：连接词 + 原子命题
六种联结词：
否定（┐）
表示：“。。。不成立”，“”
用于：表示对一个命题的否定，写成┐p
🌰：
p:2是素数
┐p：2不是素数
| p | ┐p |
| F | T |
| T | F |
合取（∧）
表示：且关系
🌰：
p:小王能踢球
q：小王能唱歌
p∧q：小王既能踢球又能唱歌
| p | q | p∧q |
| F | F | F |
| T | F | F |
| F | T | F |
| T | T | T |
析取（∨）
表示：或者关系
🌰：
p:灯泡坏了
q:线路有故障
p∨q:灯泡坏了或者线路有故障
| p | q | p∨q |
| F | F | F |
| F | T | T |
| T | F | T |
| T | T | T |
异或（⊻）
表示：两个命题不能同时都成立
例子：
p:第一节上数学
q:第一节上英语
p⊻q:第一节上数学或者上英语
| p | q | p⊻q |
| F | F | F |
| F | T | T |
| T | F | T |
| T | T | F |
蕴涵（→）
表示：表示如果。。。则。。。
🌰：
p:缺少水分
q:植物会死亡
p→q:如果确实缺少水分，植物会死亡
| p(小王发达了) | q（送大家房子） | p→q(如果小王发达了，送大家房子) |
| F | F | T(因为小王没有发达，所以无法判断q是否会发生，所有命题为真) |
| F | T | T |
| T | F | F |
| T | T | T |
等价（↔）
表示：当且仅当，互为充要条件
🌰：
p:三角形A是等边三角形
q:三角形A是等腰三角形
p↔q：三角形A即是等边三角形，又是等腰三角形
| p | q | p↔q |
| F | F | T |
| F | T | F |
| T | F | F |
| T | T | T |
完整的真值表
| p | q | p∧q | p∨q | p⊻q | p→q | p↔q |
| F | F | F | F | F | T | T |
| F | T | F | T | T | T | F |
| T | F | F | T | T | F | F |
| T | T | T | T | F | T | T |
复合命题（合式公式）
定义：
a.单个命题变元是合式公式
b.若A是合式公式，则┐A是合式公式。
c.若A和B是合式公式，则p∧q、p∨q、p→q、p↔q都是合式公式
d.当且仅当有限次的应用a、b、c所得到的含有命题变元、联结词和括号的符号串是合式公式
运算顺序约定：
运算顺序优先级：┐、∧、∨、→、↔，相同的运算符按从左到右依次序计算，优先计算括号里的内容
公式(┐p→q)∨q的真值表如下
| p | q | ┐p | ┐p→q | (┐p→q)∨q |
| F | F | T | F | F |
| F | T | T | T | T |
| T | F | F | T | T |
| T | T | F | T | T |
永真命题：公式中的命题变量无论如何代入，公式对应的真值恒为T
永假命题：公式中的命题变量无论如何代入，公式对应的真值恒为F
一般命题公式：既不是永真命题也不是永假命题
等值式
等值公式定义
定义：给定两个命题A和B，设p1,p2,p3...pn为所有出现在A、B中的原子命题，那么给p1,p2,p3...pn任一组真值指派，A和B的真值都相同，则称A和B等价，记做A=B
拿来即用的等价公式
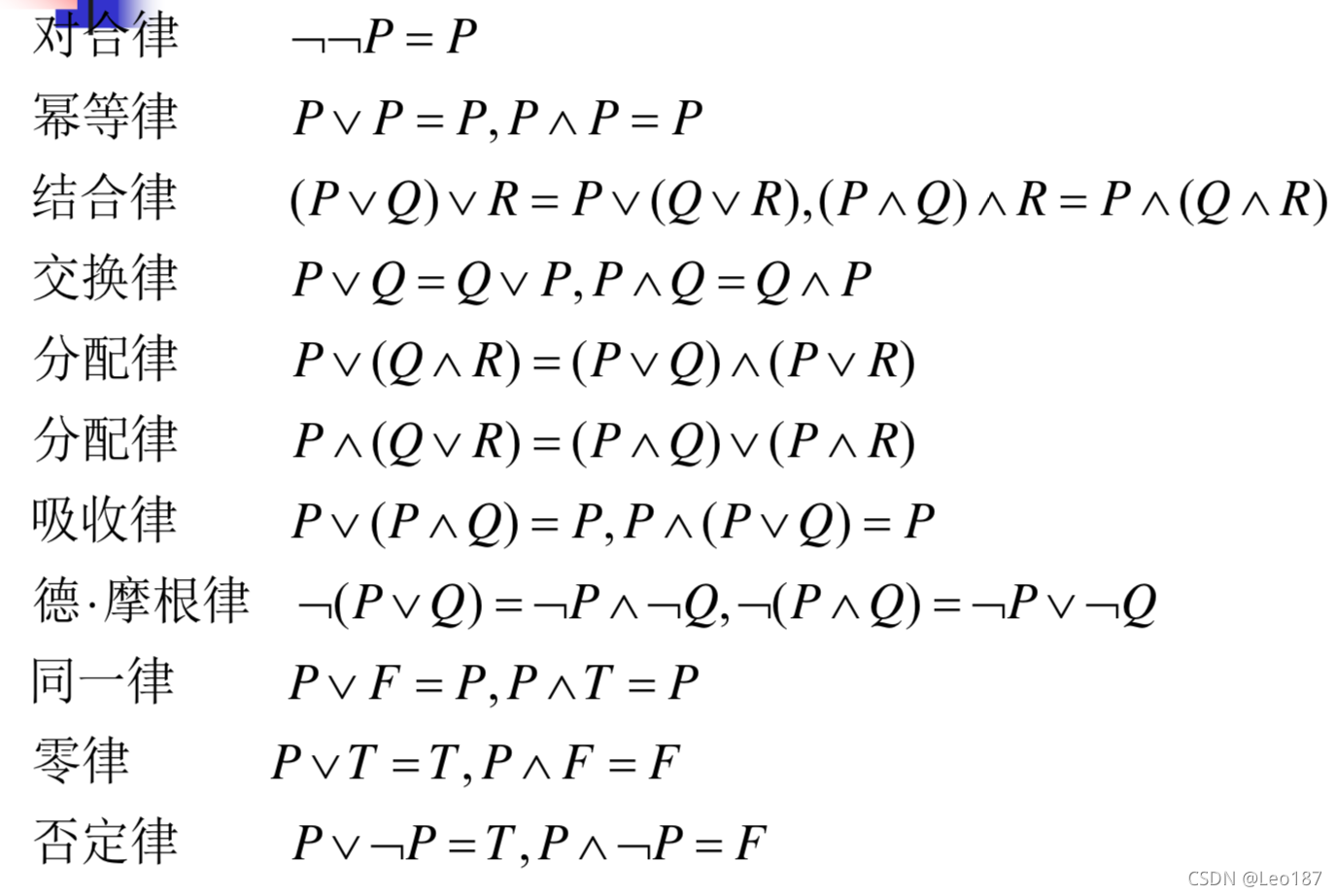
判断命题逻辑等价的方法：
- 真值表（考试力荐）
- 命题公式的演算：a.基本等值定理 b.公式的代入不变性 c.等值关系的传递性
等值公式的性质
重言式与矛盾式
例子：
| p | ┐pVp(永真) | ┐p^p(永假) |
| F | T | F |
| T | T | F |
置换式：A(p1...pn)是命题公式，如果用合式公式X替换某个Pi，其余变元不变，替换后得到的新的公式B，则称B是A(p1...pn)的置换式
永真式的性质：
- 如果A是永真式，则┐A是永假式
- 如果A、B是永真式，则p∧q、 p∨q、p⊻q、p→q、p↔q也都是永真式
- 如果A是永真式，则A的置换式也都是永真式
重言蕴含式
定义：如果p→q是重言式，则称A永真蕴涵B，记作A=>B
解释：当A为真时，B也为真
| p∧q=>p | p∧q为真的条件是p和q都为真，所以得出p为真 | p∧q=>p | 同理 |
| p=>p∨q | p为真时，p析取任何命题都为真 | q=>p∨q | 同理 |
| ┐p=>p→q | ┐p为真代表p为假，假命题的所有蕴涵式都为真 | ┐q=>p→q | 同理 |
| ┐(p→q)=>p | p→q为假，当且仅当p位真 | ┐(p→q)=>┐q | 同理 |
| p,q=>p∧q | p、q都为真，合取为真 | ┐p∧（p∨q）=>q | p假q真 |
| p∧（p→q）=>q | q为真 | ┐q∧（p→q）=>p | q为真p为假 |
| （p→q）∧（q→r）=>p→r |
1.p真，q真，r真 2.p假， |
（p∨q）∧（p→r）∧(q→r）=>r |
1.p真，r真 2.p假，q真，r真 |
| p→q=>（p∨c）→（q∨c） |
1.p真，q真 2.p假，c真 3.p假，c假 |
p→q=>（p∧c）→（q∧c） | 同理 |
范式
范式就是命题公式形式的规范形式。这里约定范式中只含联结词
简单合取式：用∧联结命题变元或变元的否定构成的式子
简单析取式：用∨联结命题变元或变元的否定构成的式子
析取范式：如果公式写成A1∨A2∨...∨An其中每个Ai是合取式，称之为A的析取范式
合取范式：如果公式写成A1∧A2∧...∧An其中每个Ai是析取式，称之为A的合取范式
范式定理：任一命题公式都存在与之等值的析取范式和合取范式
范式求法
小项：在一个又n个命题变元的合取式中，每个变元或该变元的否定仅出现一次，称这个合取式是个小项
主析取范式：析取范式A1∨A2∨...∨An其中每个Ai都是小项，称之为主析取范式
大项：在一个又n个命题变元的析取式中，每个变元或该变元的否定仅出现一次，称这个析取式是个小项
主合取范式：合取范式A1∧A2∧...∧An其中每个Ai都是大项，称之为主合取范式
谓词逻辑
个体词：指研究对象中可以独立存在的具体或抽象的客体。
谓词的定义：命题去掉主语，剩余部分叫做谓词
量词：个体变项之间的数量关系
分类 全称量词 ∀（All-A倒写）、存在量词∃（Exist-E反写）
基本两次等值定律
个体域有限 D= {a1,a2,a3....an}
∀xA(x)<=>A（a1）∧A（a2）∧A（a3）...∧A（an）
∃xA(x)<=>A（a1）∨A（a2）∨A（a3）...∨A（an）
量词否定等值式
┐∀xA(x)<=>∃x┐A（x）
┐∃xA(x)<=>∀┐A（x）
量词分配律
∀x（A(x)∧B(x)）<=>∀xA(x)∧∀xB(x)
∃x（A(x)∨B(x)）<=>∃xA(x)∨∃xB(x)
量词扩张/收缩律
∀x（A∨B(x)）<=>A∨∀xB(x)
∀x（A∧B(x)）<=>A∧∀xB(x)
∃x（A∨B(x)）<=>A∨∃xB(x)
∃x（A∧B(x)）<=>A∧∃xB(x)
腾讯云面向开发者汇聚海量精品云计算使用和开发经验，营造开放的云计算技术生态圈。
更多推荐
6
0- 0
已为社区贡献2条内容
所有评论(0)