指数增长模型
指数增长模型:(exponential growth model) 指数模型是一个早就用于描述生物群体增长的简单模型。该模型假设在研究的时间范围内,只有生殖现象而没有死亡现象,而且生物群体可以获得无限的生长条件。又称Malthns方程(1798)。将指数方程用于描述病害的增长,其微分方程为: (4.1) 式中:x
指数增长模型:(exponential growth model)
指数模型是一个早就用于描述生物群体增长的简单模型。该模型假设在研究的时间范围内,只有生殖现象而没有死亡现象,而且生物群体可以获得无限的生长条件。又称Malthns方程(1798)。将指数方程用于描述病害的增长,其微分方程为:
![]() (4.1)
(4.1)
式中:x为病害数量;dx/dt为单位时间(日)新增病害数量;re是病害指数增长速率。方程经积分成指数式:
![]() (4.2)
(4.2)
式中x0为积分常数,这里代表t=0时的初始病情,xt为经过t时间后的病情,re为指数增长率,e为自然对数的底(e=2.71828)。该方程如以x(纵座标)对t(横座标)作图,则相关曲线呈“J”字型。
在方程两边取对数,可以使方程(4.2)转化成直线方程:
![]() (4.3)
(4.3)
以ln(x)对t作图,则直线的斜率为re,截距为ln(x0),re和ln(x0) 可通过线性回归估计。通过田间调查,如知道初始病情x0和t时的病情xt,或t2时的x2和t1时的x1,则可将(4.3)式变换为(4.4)式,计算两个时间间隔的指数增长率re 。
![]()
指数模型的假设条件是:① 只考虑生殖率不考虑死亡率,对病害而言,只考虑新生病斑的发生,不考虑老病斑的消亡和报废;② 生物生存条件无限,群体可无限增大,对病害而言,可供侵染的寄主组织是无限的;③ 环境条件是稳定的,增长率不随时间而改变。实际上,可供侵染的寄主组织不可能无限,当病害数量不断增多,继续可侵染的寄主组织就逐渐减少,不考虑病害增长过程中自我抑制作用,是该模型最明显的不合理之处。所以,指数模型只能在发病初期(病害数量<0.05),可供侵染的寄主组织很多,即自我抑制作用很小时才能应用,而病害数量上升后,只能应用逻辑斯蒂模型。
指数增长[编辑]
指数增长(包括指数衰减)指一个函数的增长率与其函数值成比例。在定义域为离散的且等差的情况下,也称作几何增长或几何衰减(函数值是一个等比数列)。
指数增长模型也称作马尔萨斯增长模型。
基本公式[编辑]
变量x指数地依赖时间t,若
其中常数a是x的初始值,
并且,常数b是正的增长率,τ为x增长b倍所需时间:
若τ > 0且b > 1,则x为指数增长。若τ < 0且b > 1,或τ > 0且0 < b < 1,则x为指数衰减。
微分方程[编辑]
则称t时刻x的增长率与函数值x(t)成正比,且初值为:
对于 微分方程可以使用分离变量法求解:
微分方程可以使用分离变量法求解:
考虑到给定初值:
这种解法对于 同样适用。
同样适用。
引用[编辑]
参考文献[编辑]
- Meadows, Donella H., Dennis L. Meadows, Jørgen Randers, and William W. Behrens III. (1972) The Limits to Growth. New York: University Books. ISBN 0-87663-165-0
- Porritt, J. Capitalism as if the world matters, Earthscan 2005. ISBN 1-84407-192-8
- Thomson, David G. Blueprint to a Billion: 7 Essentials to Achieve Exponential Growth, Wiley Dec 2005, ISBN 0-471-74747-5
- Tsirel, S. V. 2004. On the Possible Reasons for the Hyperexponential Growth of the Earth Population. Mathematical Modeling of Social and Economic Dynamics / Ed. by M. G. Dmitriev and A. P. Petrov, pp. 367–9. Moscow: Russian State Social University, 2004.
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容


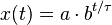
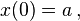

 满足
满足




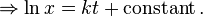










所有评论(0)