最长公共子序列-动态规划

定义描述若给定序列X={x1x_1x1,x2x_2x2,…,xmx_mxm}，则另一序列Z={z1z_1z1,z2z_2z2,…,zkz_kzk} 是X的子序列，是指存在一个严格递增下标序列{i1i_1i1,i2i_2i2,…,iki_kik}使得对于所有j=1,2,…,k有：zjz_jzj= xijx_{i_j}xij 。例如，序列Z={B，C，D，B}是序列X={A

迷雾总会解

2557人浏览 · 2020-07-02 01:20:42

迷雾总会解 · 2020-07-02 01:20:42 发布

定义描述

若给定序列X={ $x_1$ , $x_2$ ,…, $x_m$ }，则另一序列Z={ $z_1$ , $z_2$ ,…, $z_k$ } 是X的子序列，是指存在一个严格递增下标序列{ $i_1$ , $i_2$ ,…, $i_k$ }使得对于所有j=1,2,…,k有： $z_j$ = $x_{i_j}$ 。

例如，序列Z={B，C，D，B}是序列X={A，B，C，B，D，A，B}的子序列，相应的递增下标序列为{2，3，5，7}
在这里插入图片描述

给定2个序列X和Y，当另一序列Z既是X的子序列又是Y的子序列时，称Z是序列X和Y的公共子序列。

最长公共子序列：例如，序列X={A，B，C，B，D，A，B}，Y={B，D，C，A，B，A} ，{B，C，A}是X与Y的公共子序列，但不是最长公共子序列；{B，C，B，A}也是X与Y的公共子序列，但它是X与Y的最长公共子序列，因为X与Y没有长度大于4的公共子序列。

问题描述

给定2个序列X={ $x_1$ , $x_2$ ,…, $x_m$ }和 Y={ $y_1$ , $y_2$ ,…, $y_n$ }，找出X和Y的最长公共子序列。

分析最优解的结构

设序列X={ $x_1$ , $x_2$ ,…, $x_m$ }和Y={ $y_1$ , $y_2$ ,…, $y_n$ }的最长公共子序列为Z={ $z_1$ , $z_2$ ,…, $z_{k-1}$ , $z_k$ } ，则：

在这里插入图片描述

2个序列的最长公共子序列包含了它们前缀的最长公共子序列。
最长公共子序列问题具有最优子结构性质。
最优子结构性质：问题最优解，是否包含了子问题的最优解。

(1)当 $x_m$ = $y_n$

子问题变为Xm-1 ={ $x_1$ , $x_2$ ,…, $x_{m-1}$ }和Yn-1 ={ $y_1$ , $y_2$ ,…, $y_{n-1}$ }的最长公共子序列。

为了验证整个问题最优解Z是否包含子问题Xm-1和Yn-1最优解，就要验证 $Z_{k-1}$ ={ $z_1$ , $z_2$ ,…, $z_{k-1}$ }是否是子问题Xm-1和Yn-1的最长公共子序列（即：验证Zk-1是否是Xm-1和Yn-1长度为k-1的公共子序列）。

证明：若Xm-1和Yn-1有长度大于k-1的公共子序列W，则将xm加在W尾部产生X和Y的长度大于k的公共子序列，与题干中X和Y的最长公共子序列长度为k矛盾，故Zk-1是Xm-1和Yn-1的最长公共子序列

(2)当 $x_m$ ≠ $y_n$ ,且 $z_k$ ≠ $x_m$

子问题变为Xm-1 ={ $x_1$ , $x_2$ ,…, $x_{m-1}$ }和Y ={ $y_1$ , $y_2$ ,…, $y_{n}$ }的最长公共子序列。

为了验证整个问题最优解Z是否包含子问题Xm-1和Y最优解，就要验证 $Z_{k}$ ={ $z_1$ , $z_2$ ,…, $z_{k}$ 是否是子问题Xm-1和Y的最长公共子序列（即：验证Z是否是Xm-1和Y长度为k的公共子序列）。

证明：若Xm-1和Y有长度大于k的公共子序列W，则W也是X和Y的长度大于k的公共子序列，这与Z是X和Y的最长公共子序列矛盾。

(3)当 $x_m$ ≠ $y_n$ ,且 $z_k$ ≠ $y_n$

子问题变为X ={ $x_1$ , $x_2$ ,…, $x_{m}$ }和 $Y_{n-1}$ ={ $y_1$ , $y_2$ ,…, $y_{n-1}$ }的最长公共子序列。

就要验证 $Z_{k}$ ={ $z_1$ , $z_2$ ,…, $z_{k}$ 是否是子问题X和Yn-1的最长公共子序列

证明过程与（2）相似。

在这里插入图片描述

2个序列的最长公共子序列包含了它们前缀的最长公共子序列
最长公共子序列问题具有最优子结构性质

子问题的递归结构

找序列X={ $x_1$ , $x_2$ ,…, $x_m$ }和Y={ $y_1$ , $y_2$ ,…, $y_n$ }的最长公共子序列为Z={ $z_1$ , $z_2$ ,…, $z_{k-1}$ , $z_k$ } ，递归执行如下：

(1)若 $x_m$ = $y_n$

在这里插入图片描述

(2)若 $x_m$ ≠ $y_n$

在这里插入图片描述

a）和 b）这两个公共子序列中较长者即为X和Y的最长公共子序列。

递归结构

由最优子结构性质建立子问题最优值的递归关系

用c[i][j]记录序列 $X_i$ 和 $Y_j$ 的最长公共子序列的长度，其中， $X_i$ ={ $x_1$ , $x_2$ ,…, $x_i$ }； $Y_j$ ={ $y_1$ , $y_2$ ,…, $y j$ }

当i=0或j=0时，空序列是Xi和Yj的最长公共子序列。故C[i][j]=0。

由最优子结构性质可建立递归关系如下：
在这里插入图片描述

子问题重叠性质

最长公共子序列问题具有子问题重叠性质；

例如，若xm≠yn，找X和Y的最长公共子序列，要计算Xm-1和Y以及X和Yn-1的最长公共子序列，而这两个都包含一个公共子问题，即计算Xm-1和Yn-1的最长公共子序列。

计算最优值

子问题空间中，共有θ(mn)个不同的子问题.
用动态规划算法自底向上地计算最优值能提高算法的效率。
用c[i][j]记录序列 $X_i$ 和 $Y_j$ 的最长公共子序列的长度，其中， $X_i$ ={ $x_1$ , $x_2$ ,…, $x_i$ }； $Y_j$ ={ $y_1$ , $y_2$ ,…, $y j$ }
b[i][j]记录c[i][j]由哪一个子问题得到。

在这里插入图片描述

核心算法

用c[i][j]记录序列 $X_i$ 和 $Y_j$ 的最长公共子序列的长度，其中， $X_i$ ={ $x_1$ , $x_2$ ,…, $x_i$ }； $Y_j$ ={ $y_1$ , $y_2$ ,…, $y j$ }
b[i][j]记录c[i][j]由哪一个子问题得到。

在这里插入图片描述
三种情况下b[i][j]的取值

构造最长公共子序列

LCSLength只是计算出最优值，并未给出最优解，然而数组b可用于快速构造两个序列的最长公共子序列：

b[i][j]=1时表示Xi和Yj的最长公共子序列是由Xi-1和Yj-1的最长公共子序列加上xi所得到；
b[i][j]=2时表示Xi和Yj的最长公共子序列与Xi-1和Yj的最长公共子序列相同；
b[i][j]=3时表示Xi和Yj的最长公共子序列与Xi和Yj-1的最长公共子序列相同。

根据b的内容打印出最长公共子序列

核心算法

在这里插入图片描述

例子

给定两个序列X={B,C,D,A}，Y={A,B,C,B}，请采用动态规划策略。求出其最长公共子序列，要求给出过程。
在这里插入图片描述

算法的改进

算法lcsLength和lcs中，可进一步将数组b省去。

事实上，数组元素c[i][j]的值仅由c[i-1][j-1]，c[i-1][j]和c[i][j-1]这3个数组元素的值所确定。
对于给定的数组元素c[i][j]，可仅借助于c本身确定c[i][j]的值是由c[i-1][j-1]，c[i-1][j]和c[i][j-1]中哪一个值所确定的。

给定两个序列X={B,C,D,A}，Y={A,B,C,B}，请采用动态规划策略求出其最长公共子序列，要求给出过程。

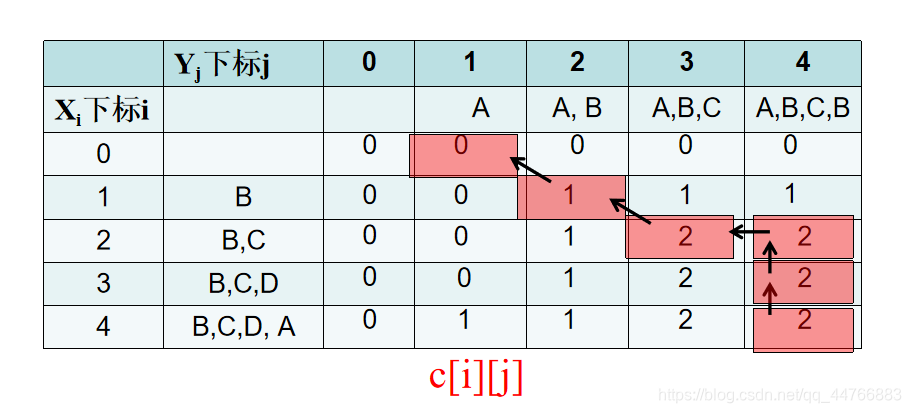
在这里插入图片描述
参照算法分析：

for (i = 1; i <= m; i++)
     for (j = 1; j <= n; j++) {
         if (x[i]==y[j]) { 
               c[i][j]=c[i-1][j-1]+1; b[i][j]=1;}
         else if (c[i-1][j]>=c[i][j-1]) {
               c[i][j]=c[i-1][j]; b[i][j]=2;}
         else {
               	c[i][j]=c[i][j-1]; b[i][j]=3;}
      }
}

[4,4]开始，此时为2。比较[4,3]和[3,4]，与[4,4]的值相同，说明没有新增公共字符。又[3,4]=[4,3]，从算法中可以看出此时下一步应该是[i-1,j],即[3,4]
[3,4]开始,此时为2。比较[3,3]和[2,4]，与[3,4]的值相同，说明没有新增公共字符。又[3,3]=[2,4]，从算法中可以看出此时下一步应该是[i-1,j],即[2,4]
[2,4]开始,此时为2。比较[2,3]和[1,4]，有一个与[2,4]相同，说明没有新增公共字符。又[2,3]>[1,4]，从算法中可以看出此时下一步应该是[i,j-1],即[2,3]
[2,3]开始,此时为2。比较[2,2]和[1,3]，都与[2,3]不同，说明此时新增了公共字符。从算法中可以看出此时下一步应该是[i-1,j-1],即[1,2]
[1,2]开始,此时为2。比较[1,1]和[0,2]，都与[1,2]不同，说明此时新增了公共字符。从算法中可以看出此时下一步应该是[i-1,j-1],即[0,1]
此时x=0,算法结束.

最长公共子序列：｛ＢＣ｝

扩展

如果只需要计算最长公共子序列的长度，则算法的空间需求可大大减少。

事实上，在计算c[i][j]时，只用到数组c的第i行和第i-1行。
用2行的数组空间就可以计算出最长公共子序列的长度。
进一步的分析还可将空间需求减至O(min(m,n))。

完整算法

#include<bits/stdc++.h>
using namespace std;
char x[1020], y[1020], z[1020];
int c[1020][1020], b[1020][1020];
int m, n;
void LCSLength()
{
    memset(c, 0, sizeof(c));
    memset(b, 0, sizeof(b));
    for(int i = 1; i <= m; ++i)
    {
        for(int j = 1; j <= n; ++j)
        {
            if(x[i] == y[j])
            {
                c[i][j] = c[i - 1][j - 1] + 1;
                b[i][j] = 1;
            }
            else if(c[i - 1][j] >= c[i][j - 1])
            {
                c[i][j] = c[i - 1][j];
                b[i][j] = 2;
            }
            else
            {
                 c[i][j] = c[i][j - 1];
                 b[i][j] = 3;
            }
        }
    }
}
void LCS(int i, int j)
{
   if(i == 0 || j == 0)
        return ;
   if(b[i][j] == 1)
   {
       LCS(i - 1, j - 1);
       cout << x[i];
   }
   else if(b[i][j] == 2)
   {
       LCS(i - 1, j);
   }
   else
   {
       LCS(i, j - 1);
   }
}
void Input()
{
    cout<<"请输入第一个序列(字母中间不要空格)：";
    gets(x);

    cout<<"请输入第二个序列(字母中间不要空格)：";
    gets(y);

    m = strlen(x);
    n = strlen(y);
    strcpy(x + 1, x);//为了方便，0号位置不放元素
    strcpy(y + 1, y);
}
int main()
{
  Input();
  LCSLength();
  LCS(m, n);
}