遗传算法（GA）

遗传算法（Genetic Algorithm，GA）是一类模仿生物进化过程的搜索启发式算法。它们是由约翰·霍兰德（John Holland）在20世纪70年代初提出的。遗传算法通过自然遗传机制（如选择、交叉、变异等）的模拟，对问题的潜在解进行进化，以期找到或逼近最优解。基本原理是类比达尔文进化论—“物竞天择，适者生存”其实很好理解，学过生物的都知道达尔文进化论的大概内容：变异：种群中单个样本的特征

Ba797

4360人浏览 · 2024-09-06 21:34:34

Ba797 · 2024-09-06 21:34:34 发布

遗传算法（GA）

一、什么是遗传算法？

遗传算法（Genetic Algorithm，GA）是一类模仿生物进化过程的搜索启发式算法。它们是由约翰·霍兰德（John Holland）在20世纪70年代初提出的。遗传算法通过自然遗传机制（如选择、交叉、变异等）的模拟，对问题的潜在解进行进化，以期找到或逼近最优解。

基本原理是类比达尔文进化论—“物竞天择，适者生存”

其实很好理解，学过生物的都知道达尔文进化论的大概内容：

变异：种群中单个样本的特征（性状，属性）可能会有所不同，这导致了样本彼此之间有一定程度的差异。

遗传：某些特征可以遗传给其后代。导致后代与双亲样本具有一定程度的相似性。

选择：种群通常在给定的环境中争夺资源。更适应环境的个体在生存方面更具优势，因此会产生更多的后代。

下面我们逐个进行讲解（有一篇文章好玩又很好理解，可以去看看https://zhuanlan.zhihu.com/p/35986593）

二、基本步骤

GA通过迭代来优化目标函数的参数，直到目标函数满足一定条件时结束。迭代对目标函数的连续性并无要求，也就是说算法的迭代并不基于目标函数在当前参数下的梯度等连续性质。算法的转化思想是将所有待优化参数看做生物染色体，单个参数看做染色体上对应位置的基因，而目标函数看做生物对生存环境的适应度。上图可知，遗传算法主要内容就是：

（1）随机生成一定数量的生物个体，它们的染色体各不相同，因此在生存环境中的适应度也不同。也就是说，这些随机生成的参数对目标函数的满足度各不相同。

（2）根据个体对环境的适应度，适者生存。选择适应度较高的一部分个体，生存下来，有资格繁殖下一代，剩下的都死在这一代。当然这里也可以随机少量选择一些“幸运”的适应度较低的个体，让它们也能参与繁殖，增加多样性。

（3）对选出的个体进行两两“交配”，交配就是让它们DNA中对应位置的基因进行交叉和变异产生新的个体（不知道交叉和变异的回去读高中生物书），得到下一代。具体的交配和交叉变异策略下面再详细介绍。

（4）在新的一代，对所有个体进行判断，是否已经有个体满足目标函数的终极条件。有就结束迭代，否则回到1。

三、算法概念

串：这里的串可不是杂种，而是表示生物个体的染色体，通常是二进制串，或根据优化需要使用其它形式的串。

**群体和群体大小：**个体的集合称为群体，串是群体的元素。群体中个体的数量称为群体大小。

基因：基因是串中的元素，用来表示个体特征。通常一个基因对应一个参数，或者在二进制编码时，一位就代表一个基因。

**基因位置：**基因在串中的位置，简称基因位。

**串结构空间：**基因任意组合所形成的串集合，也就是在当前优化背景下所有可能的串的集合。

适应度：表示某一个体对环境的适应程度，用一个函数表示，通常就是待优化的目标函数。

以下图为例：一条染色体可以表示为二进制串，其中每个位代表一个基因

四、算法详解

1、编码

实际问题参数集实际上就是待优化的参数，可以编码为各种形式的串，以便进行上述的遗传迭代。

编码必须是可逆的，也就是参数可以编码成串，串可以解码为参数，串与参数之间应该是一一对应的，从而每次迭代都能解码并计算个体的适应度。并且GA的编码可以有个十分广泛的理解，不局限于简介中对待优化参数的编码。比如，在分类问题，串可解释为一个规则，即串的前半部为输入或前件，后半部为输出或后件、结论。因此，遗传算法可以对大量的问题进行建模，只要把问题的条件啊，约束啊，参数啊全都一股脑地编码丢进去“进化”就好了，这也是为什么它在数学建模比赛中如此热门的原因。

编码方式主要有二进制编码、格雷编码、实数编码等。二进制编码就是把参数都转换为二进制，然后排成一排，编码的每一位都看做一个基因。实数编码实际上就是不编码，当参数都为实数而且很多时，就可以直接把这些实数参数作为染色体基因。下面介绍格雷码。

格雷编码

格雷编码是对二进制编码进行变换后所得到的一种编码方法，它要求两个连续整数的编码之间只能有一个码位不同，其余码位都是完全相同的。因此，格雷码解决了二进制编码的汉明悬崖问题。二进制编码与格雷码之间的转换如下：

$b_{1}, b_{2}, \ldots, b_{n} ，对应的格雷串为 a_{1}, a_{2}, \ldots, a_{n} ，则从二进制编码到格雷编码的变换为:$

$a_{i}=\left\{\begin{array}{ll} b_{i}, & i=1 \\ b_{i-1} \oplus b_{i}, & i>1 \end{array}\right.$

其中 $\oplus$ 为异或运算。格雷码到二进制编码的变换为: $b_{i}=\left(\sum_{j=1}^{i} a_{i}\right) \bmod 2$

如下图所示：外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

2、适应度函数（Fitness function）

在算法的每次迭代中，使用适应度函数（也称为目标函数）对个体进行评估。目标函数是用于优化的函数或试图解决的问题。

适应度得分更高的个体代表了更好的解，其更有可能被选择繁殖并且其性状会在下一代中得到表现。随着遗传算法的进行，解的质量会提高，适应度会增加，一旦找到具有令人满意的适应度值的解，终止遗传算法。

原始适应度函数直接将待求解问题的目标函数f(x)定义为算法的适应度函数。比如求解极值问题

$\max _{x \in[a, b]} f(x)$

直接将f(x)作为原始适应度函数。

3、选择

选择模拟了生物进化中的 “适者生存”，根据当代的个体的适应度按概率选出下一代，适应度越高，则被选择的概率也越大。一般使用最广的策略是**轮盘赌策略**，如图所示：

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

所占份额越多选中的概率就越大，但是一般不直接将适应度最大的若干个个体作为下一代，是因为这样可能会导致算法过早陷入局部最优解。在遗传算法里面这种现象称为 “早熟（premature）”。

假如当代的个体总数是 } $M$ ，而个体 $a_{i}$ 的适应度是 $f_{i}$ ，则个体 $a_{i}$ 被选择到下一代的概率是 :

$p_{i}=\frac{f_{i}}{\sum_{j=1}^{M} f_{j}}$

4、交叉

交叉跟生物上的杂交是一样的，只是生物中是双螺旋结构，而遗传算法中只有一条链。原始的遗传算法只会选择一个点进行交叉，如下如所示

而假如对遗传算法进行改进，也可以在多个点进行交叉的操作

交叉（crossover）的目的是从目前的所有解中组合出更优的解，但是尝试获得更优解的同时，也可能丢掉目前得到的最优解。而这也是传统的遗传算法无法收敛到全局最优的一个原因

交叉是按照一定的概率进行的，这个概率也需要人为设定，假如设得过大边很容易将当前的最优解破坏掉，并且容易陷入早熟 (premature)，而设得过小时则很难从当前的可行解中组合出更优的解。

如下图所示：

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

5、变异

变异（mutation）跟生物中的变异也一样，随机改变染色体中的某一位，如下所示就是一个变异的示例

变异也是按照一定的概率进行的，这个概率也需要人为设定，而且这个概率一般会设置得比较小，如果设得较大时，就变成了类似随机搜索（random search）的方法；但是如果设得太小的时候，就会造成生物中的基因漂变 (genetic drift) 的现象，从而导致收敛到一个局部最优。

变异的主要作用是为了防止算法收敛到一个局部最优解。假如将找到最优解比作在多座山峰中找到最高的那一座，那么交叉就类似同一座山峰下的多个基因合力爬上山顶，而变异就类似于从一座山峰调到另外一座山峰，目的就是为了防止当前的山峰是一个局部最优解而将算法其作为一个全局最优解。

五、性能优化

1、精英主义选择(Elitism Strategy)

防止进化迭代过程中产生的最优解被交叉和变异破坏, 将每一代的最优解原封不动地复制到下一代中.

2、插入

在原来的选择, 交叉, 变异三种基本操作的基础上增加一个插入操作, 插入操作将染色体中的某个随机的片段移位到另一个随机的位置.

具体的优化请自行查询

六、遗传算法的优缺点

遗传算法的优点

全局搜索能力强：遗传算法通过选择、交叉和变异等操作，能够有效避免局部最优解，具有较强的全局搜索能力。
适应性强：不依赖具体问题的数学特性，适用于各种优化问题，包括复杂、非线性、多维的问题。
并行处理能力：遗传算法通过操作多个个体（染色体），天然具有并行处理能力，有利于加速计算过程。
鲁棒性高：能够处理不确定性问题和随机性问题，对噪声数据或不精确的模型依然有效。
广泛应用：能够处理连续优化问题、离散优化问题、多目标优化问题等，应用范围广泛。

遗传算法的局限性

收敛速度较慢：由于遗传算法是一种启发式算法，可能需要较多的迭代才能找到接近最优解，尤其是在问题规模较大时。
早熟收敛问题：在某些情况下，算法可能陷入局部最优解，导致收敛过早，无法找到全局最优解。
参数调优复杂：遗传算法中的参数（如种群大小、变异率、交叉率）对结果影响较大，调优这些参数可能较为复杂。
不保证最优解：遗传算法是一种启发式算法，不能保证在有限的时间内找到问题的全局最优解。
计算量较大：虽然适合并行处理，但若种群规模过大或问题维度较高，计算资源消耗较大。

七、代码示例

1：对复杂数学模型求极值

$\exp \left[\frac{-(x+3)^{2}-(y-3)^{2}}{10}\right]+1.2 \exp \left[\frac{-(x-3)^{2}-(y+3)^{2}}{10}\right]+\frac{1}{5} \exp [-\cos (3 x)-\sin (3 y)]$

求上述数学模型的最大值

# %%定义函数
import time
import numpy as np


def func(X, Y):
    return np.exp((-(X + 3) ** 2 - (Y - 3) ** 2) / 10) * 2 + np.exp((-(X - 3) ** 2 - (Y + 3) ** 2) / 10) * 1.2 + np.exp(
        -np.cos(X * 3) - np.sin(Y * 3)) / 5


# %%遗传算法
time_start = time.time()
dim = 2
iterate_times = 150
individual_n = 200
p_c = 0.4
p_m = 0.15
std_var = 20
num_range = [-100, 100]


def initialize(individual_n, num_range):
    return np.random.uniform(num_range[0], num_range[1], size=[individual_n, dim])


def overlapping(a, b, pc, dim):
    T = np.random.choice(a=2, size=dim, p=[1 - pc, pc])
    for i in range(dim):
        if T[i] == 1:
            a[i], b[i] = b[i], a[i]


def variation(a, pm, dim, num_range):
    T = np.random.choice(a=2, size=dim, p=[1 - pm, pm])
    for i in range(dim):
        if T[i] == 1:
            a[i] = np.clip(np.random.normal(loc=a[i], scale=std_var), num_range[0], num_range[1])


def get_select_p(v):
    exp_v = np.exp(v)
    sum_exp_v = np.sum(exp_v)
    return exp_v / sum_exp_v


def select_and_reproduction(population, num_range):
    values = func(population[:, 0], population[:, 1])
    select_p = get_select_p(values)

    choices = np.random.choice(a=len(population), size=len(population), replace=True, p=select_p)
    new_population = population[choices]
    for i in range(int(len(new_population) / 2)):
        overlapping(new_population[2 * i], new_population[2 * i + 1], p_c, dim)
        variation(new_population[2 * i], p_m, dim, num_range)
        variation(new_population[2 * i + 1], p_m, dim, num_range)
    argmax_value = np.argmax(values)
    return values[argmax_value], population[argmax_value], new_population


population = initialize(individual_n, num_range)
times_population = np.empty([iterate_times, individual_n, dim])
max_value = 0
max_value_coordinate = []
for i in range(iterate_times):
    times_population[i] = population
    last_max_value, last_max_value_pos, population = select_and_reproduction(population, num_range)
    if last_max_value > max_value:
        max_value = last_max_value
        max_value_coordinate = last_max_value_pos
    print(i, ":  ", last_max_value)

time_end = time.time()
print('总共耗时：', time_end - time_start)
print('迭代最大值：', max_value)
print('对应坐标：', max_value_coordinate)
# %%画出种群的迭代过程
import matplotlib.pyplot as plt
import matplotlib.animation as animation

fig, ax = plt.subplots()
xdata, ydata = [], []
ln, = plt.plot([], [], 'ro', animated=True, color='black', markersize=2)


def init():
    ax.set_xlim(num_range[0], num_range[1])
    ax.set_ylim(num_range[0], num_range[1])
    ax.set_xlabel('X')
    ax.set_ylabel('Y')
    return ln,


def update(frame):
    frame = int(frame)
    xdata = times_population[frame, :, 0]
    ydata = times_population[frame, :, 1]
    ln.set_data(xdata, ydata)
    return ln,


anim = animation.FuncAnimation(fig, update, frames=np.linspace(0, iterate_times - 1, iterate_times), interval=100,
                               init_func=init, blit=True)
plt.show()

迭代过程如下图所示，最终收敛到[-3,-3]左右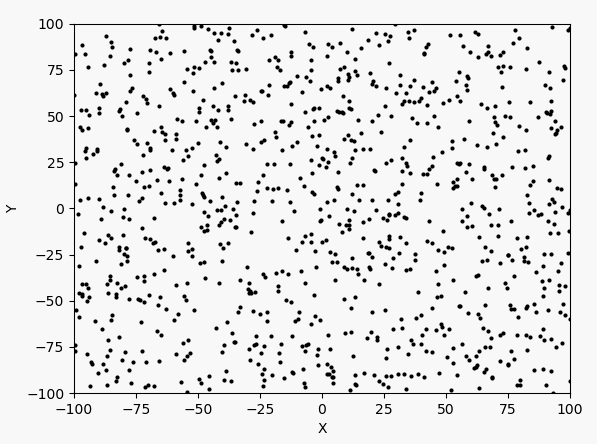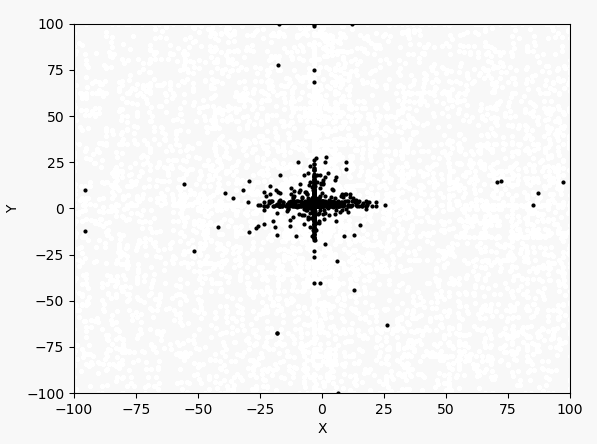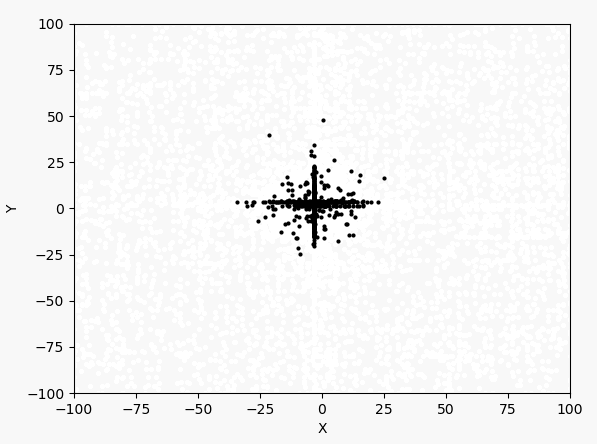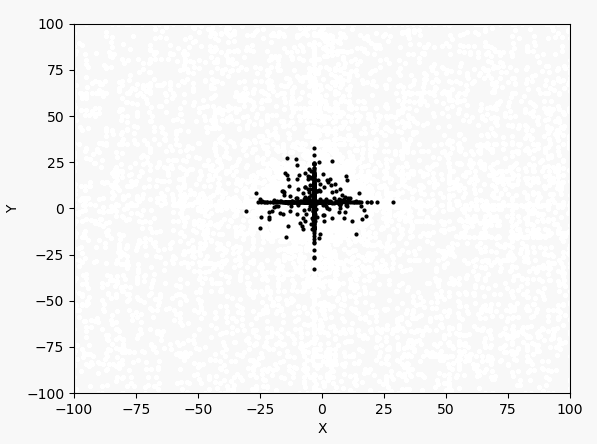

2：对心形极大值的计算

import numpy as np
import random
from scipy.optimize import fsolve
import matplotlib.pyplot as plt
import heapq
import time

# 求染色体长度
def getEncodeLength(decisionvariables, delta):
    # 将每个变量的编码长度放入数组
    # 这个要看有几个自变量，假如自变量的个数是3，那么返回的lengths的元素就有3个
    lengths = []
    for decisionvar in decisionvariables:
        uper = decisionvar[1]
        low = decisionvar[0]
        # res返回一个数组
        res = fsolve(lambda x:((uper-low)/delta-2**x+1), 30)
        # ceil()向上取整
        length = int(np.ceil(res[0]))
        lengths.append(length)
    return lengths


def getinitialPopulation(length, populationSize):
    # 根据DNA长度和种群大小初始化种群
    chromsomes = np.zeros((populationSize, length), dtype=int)
    for popusize in range(populationSize):
        # np.random.randint产生[0,2)之间的随机整数，第三个数表示随机数的数量
        chromsomes[popusize, :] = np.random.randint(0, 2, length)
    return chromsomes

# 染色体解码得到表现形的解
def getDecode(population, encodeLength, decisionVariables, delta):
    # 把染色体计算成数字
    populationsize = population.shape[0]
    length = len(encodeLength)
    decodeVariables = np.zeros((populationsize, length), dtype=float)  # 将 np.float 替换为 float
    for i, populationchild in enumerate(population):
        start = 0
        for j, lengthchild in enumerate(encodeLength):
            power = lengthchild - 1
            decimal = 0
            for k in range(start, start+lengthchild):
                decimal += populationchild[k] * (2**power)
                power = power - 1
            start = lengthchild
            lower = decisionVariables[j][0]
            uper = decisionVariables[j][1]
            decodevalue = lower + decimal * (uper - lower) / (2**lengthchild - 1)
            decodeVariables[i][j] = decodevalue
    return decodeVariables


# 得到每个个体的适应度值及累计概率
def getFitnessValue(func, decode):
    popusize, decisionvar = decode.shape
    fitnessValue = np.zeros((popusize, 1))
    for popunum in range(popusize):
        fitnessValue[popunum][0] = func(decode[popunum][0])
    probability = fitnessValue/np.sum(fitnessValue)
    cum_probability = np.cumsum(probability)
    return fitnessValue, cum_probability

def selectNewPopulation(decodepopu,cum_probability):
    m,n = decodepopu.shape
    newPopulation = np.zeros((m,n))
    for i in range(m):
        randomnum = np.random.random()
        for j in range(m):
            if(randomnum < cum_probability[j]):
                newPopulation[i] = decodepopu[j]
                break
    return newPopulation


def crossNewPopulation(newpopu, prob):
    m, n = newpopu.shape
    numbers = np.uint8(m*prob)
    if numbers %2 != 0:
        numbers = numbers + 1
    updatepopulation = np.zeros((m,n),dtype=np.uint8)
    index = random.sample(range(m),numbers)
    for i in range(m):
        if not index.__contains__(i):
            updatepopulation[i] = newpopu[i]
    j = 0
    while j < numbers:
        crosspoint = np.random.randint(0,n,1)
        crosspoint = crosspoint[0]
        updatepopulation[index[j]][0:crosspoint] = newpopu[index[j]][0:crosspoint]
        updatepopulation[index[j]][crosspoint:] = newpopu[index[j+1]][crosspoint:]
        updatepopulation[index[j+1]][0:crosspoint] = newpopu[index[j+1]][0:crosspoint]
        updatepopulation[index[j+1]][crosspoint:] = newpopu[index[j]][crosspoint:]
        j = j + 2
    return updatepopulation


def mutation(crosspopulation,mutaprob):
    mutationpopu = np.copy(crosspopulation)
    m,n = crosspopulation.shape
    mutationnums = np.uint8(m*n*mutaprob)
    mutationindex = random.sample(range(m*n),mutationnums)
    for geneindex in mutationindex:
        row = np.uint8(np.floor(geneindex/n))
        colume = geneindex % n
        if mutationpopu[row][colume] == 0:
            mutationpopu[row][colume] =1
        else:
            mutationpopu[row][colume] = 0
    return mutationpopu


def findMaxPopulation(population, maxevaluation, maxSize):
    maxevalue = maxevaluation.flatten()
    maxevaluelist = maxevalue.tolist()
    maxIndex = map(maxevaluelist.index, heapq.nlargest(100, maxevaluelist))
    index = list(maxIndex)
    colume = population.shape[1]
    maxPopulation = np.zeros((maxSize, colume))
    i = 0
    for ind in index:
        maxPopulation[i] = population[ind]
        i = i + 1
    return maxPopulation


def fitnessFunction():
    return lambda x: 10*np.sin(5*x) + 7*np.abs(x-5) + 10





def main():
    optimalvalue = []
    optimalvariables = []

    decisionVariables = [[0.0, 10.0]]
    delta = 0.0001
    EncodeLength = getEncodeLength(decisionVariables, delta)
    print(EncodeLength)

    initialPopuSize = 100
    population = getinitialPopulation(sum(EncodeLength), initialPopuSize)
    print(population)
    # 最大进化代数
    maxgeneration = 30

    # 交叉概率
    prob = 0.8

    # 变异概率
    mutationprob = 0.1

    # 新生成的种群数量
    maxPopuSize = 100

    # 用于记录最终最优个体及其适应度值
    global_optimal_value = None
    global_optimal_variable = None

    for generation in range(maxgeneration):
        decode = getDecode(population, EncodeLength, decisionVariables, delta)

        evaluation, cum_proba = getFitnessValue(fitnessFunction(), decode)

        # 记录当前代中最优个体及其目标值
        current_optimal_value = np.max(evaluation)
        current_optimal_variable = decode[np.argmax(evaluation)]

        # 比较更新全局最优解
        if global_optimal_value is None or current_optimal_value > global_optimal_value:
            global_optimal_value = current_optimal_value
            global_optimal_variable = current_optimal_variable

        newpopulations = selectNewPopulation(population, cum_proba)

        crossPopulation = crossNewPopulation(newpopulations, prob)

        mutationpopulation = mutation(crossPopulation, mutationprob)

        totalpopalation = np.vstack((population, mutationpopulation))

        final_decode = getDecode(totalpopalation, EncodeLength, decisionVariables, delta)

        final_evaluation, final_cumprob = getFitnessValue(fitnessFunction(), final_decode)

        population = findMaxPopulation(totalpopalation, final_evaluation, maxPopuSize)

        optimalvalue.append(np.max(final_evaluation))

        index = np.where(final_evaluation == max(final_evaluation))

        optimalvariables.append(list(final_decode[index[0][0]]))

        # 绘图展示种群分布情况
        decodeTemp = getDecode(population, EncodeLength, decisionVariables, delta)
        evaluationTemp, cum_probaTemp = getFitnessValue(fitnessFunction(), decodeTemp)
        plt.plot(decodeTemp, evaluationTemp, "*")
        x = np.arange(0.0, 10, 0.001)
        y = 10 * np.sin(5 * x) + 7 * np.abs(x - 5) + 10
        plt.plot(x, y)
        plt.show()
        time.sleep(1)

    # 输出最终最优解及其目标值
    print(f"最终收敛到的位置: {global_optimal_variable}")
    print(f"最终最优目标值: {global_optimal_value}")

    # 绘制适应度进化图
    x = [i for i in range(maxgeneration)]
    y = [optimalvalue[i] for i in range(maxgeneration)]
    plt.plot(x, y)
    plt.show()

    return global_optimal_value, global_optimal_variable


if __name__ == '__main__':
    optval, optvar = main()
    print("x1:", optvar[0])
    print("maxValue:", optval)