图都由顶点（Vertex）和边（Edge）有限集合而成
图分为无向图和有向图
无向图：代表边的顶点对（或序偶）是无序的，则称为无向图。代表边的无序顶点对通常用圆括号括起来，以表示一条无向边。（i，j）
有向图：表示边的顶点对（或序偶）是有序的，则称为有向图。代表边的无序顶点对通常用尖括号括起来，以表示一条有向边。<i，j>

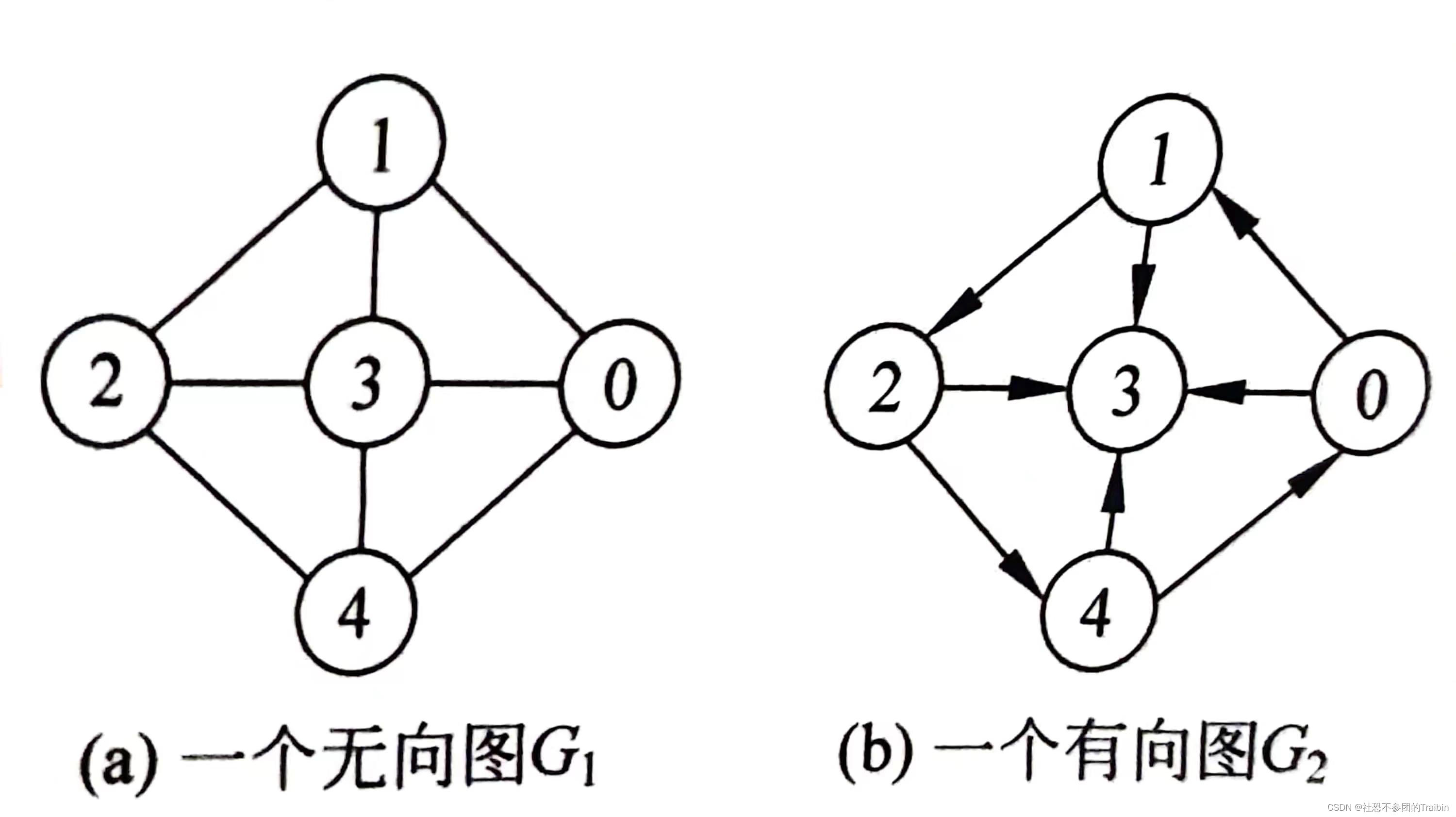图1：无向图和有向图的示意图

基本术语

1、端点和邻接点
在一个无向图中,若存在一条边(i，j),则称顶点“i”和顶点“j“为该边的两个端点，并称它们互为邻接点，即顶点”i“是顶点”j“的一个邻接点，顶点j也是顶点i的一个邻接点。
在一个有向图中，若存在一条边<i,j>，则称此边是顶点”i“的一条出边,同时也是顶点”j“的一条入边；称”i“和”j“分别为此边的起始端点(简称为起点)和终止端点(简称为终点)，并称顶点”j“是”i“的出边邻点，顶点”i“是”j“的入边邻接点。
2、顶点的度、入度和出度
在无向图中，顶点所关联的边的数目称为该顶点的度。在有向图中，顶点”i“的度又分为入度和出度，以顶点”i“为终点的入边的数目称为该顶点的入度，以顶点”i“为起点的出边的数目称为该顶点的出度。一个顶点的入度与出度的和为该顶点的度。一个图中所有顶点的度之和等于边数的两倍。因为图中的每条边分别作为两个邻接点的度各计一次。
3、完全图
若无向图中的每两个顶点之间都存在一条边 ,有向图中的每两个顶点之间都存在方向相反的两条边，则称此图为完全图。显然,含有n个顶点的完全无向图有n(n-1)/2条边，含有n个顶点的完全有向图有n(n-1)条边。
4、连通、连通图和连通分量
在无向图G中,若从顶点”i“到顶点”j”有路径,则称顶点“i”和顶点“j”是连通的。若图G中的任意两个顶点都连通，则称G为连通图，否则称为非连通图。无向图G中的极大连通子图称为G的连通分量。显然，任何连通图的连通分量只有一个，即它本身，而非连通图有多个连通分量。
4、强连通图和强连通分量
在有向图G中,若从顶点“i”到顶点“j”有路径，则称从顶点“i”到顶点“j”连通的。若图G中的任意两个顶点“i”和“j”都连通，即从顶点“i”到顶点“j”和从顶点“j”到顶点“i’都存在路径，则称图G是强连通图。有向图G中的极大强连通子图称为G的强连通分量。显然,强连通图只有一个强连通分量，即它本身，非强连通图有多个强连通分量。一般地，单个顶点自身就是一个强连通分量。
5、权和网
图中的每一条边都可以附有一个对应的数值。这种与边相关的数值称为权。权可以表示从图中顶点到另一个顶点的距商或花费的代价。边上带有权的图称为带权图。也称作网。

图的存储结构

邻接矩阵

邻接矩阵是表示顶点之间邻接关系的矩阵。设G=(V ,E)是含有n(设n>0)个顶占的图,各顶点的编号为0~n-1,则G的邻接矩阵数组A是n阶方阵,其定义如下
如果G是不带权图(或无权图),则:

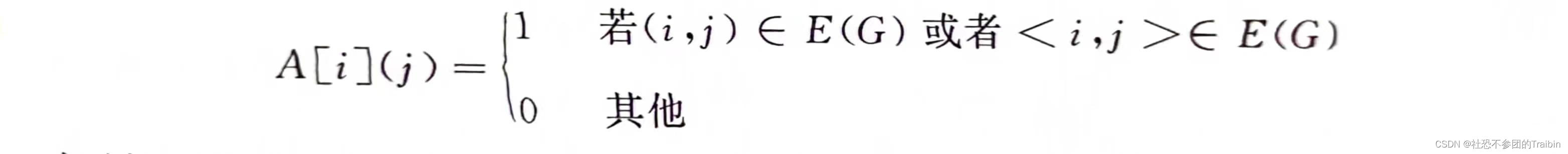如果G是带权图(或有权图)，则:

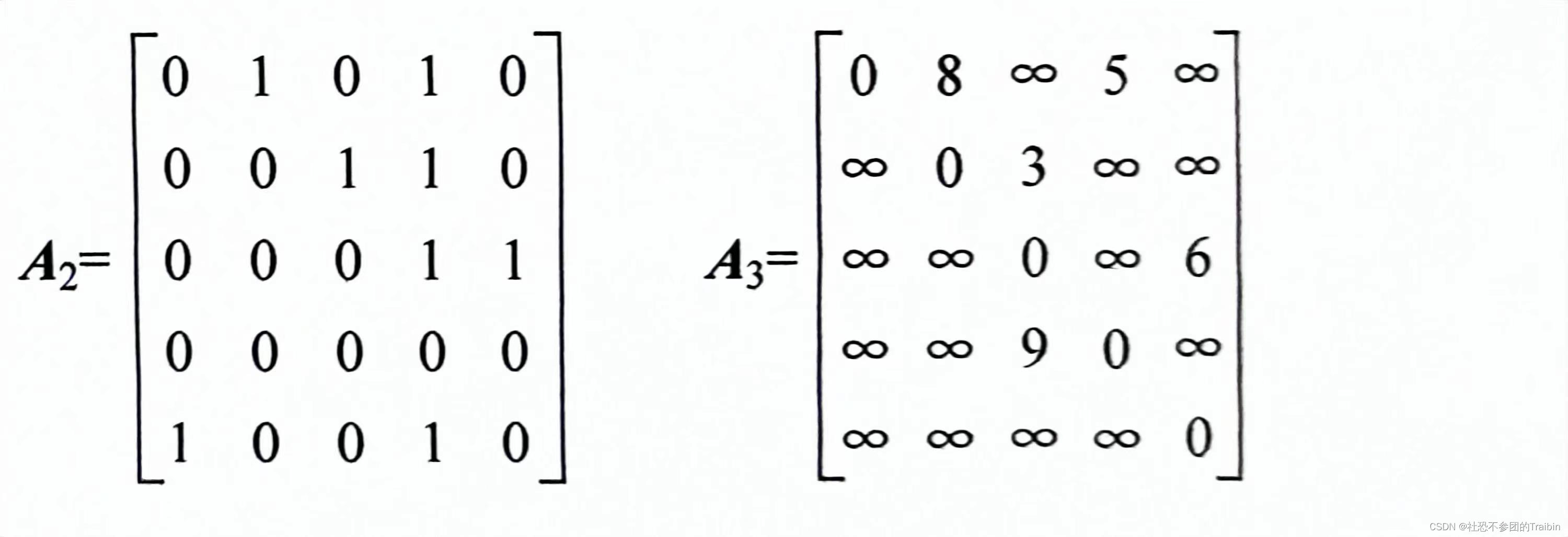图2：2个邻接矩阵

邻接矩阵的基本结构运行算法代码

const int MAXV=100;        //图中最多的顶点数
const int INF=0x3f3f3f3f;    //用INF表示∞
class MaxGraph
{
public:
    int edges[MAXV][MAXV];    //邻接矩阵数组，假设元素为int
    int n,e;                    //顶点数和边数
    string vexs[MAXV];        //存放顶点信息
};

图的邻接矩阵存储结构的特点如下:
1、图的邻接矩阵表示是唯一的。
2、对于含有n个顶点的图，在采用邻接矩阵存储时，无论是有向图还是无向图，也无论边的数目是多少,其存储空间均为O（n^2）所以邻接矩阵适合干存储边数较多的调密图
3、无向图的邻接矩阵一定是对称矩阵，因此在顶点个数n很大时可以采用对称矩阵的压缩存储方法减少存储空间。有向图的邻接矩阵不一定是对称矩阵。
4、对于无向图，邻接矩阵的第i行(或第i列)非零/非∞元素的个数正好是顶点i的度；对于有向图，邻接矩阵的第i行(或第i列)非零/非∞元素的个数正好是顶点i的出度(或入度)
5、用邻接矩阵存储图时，确定任意两个顶点之间是否有边相连的时间为0(1）

邻接矩阵代码实现

创建邻接矩阵

void CreateMatGraph(int a[][MAXV],int n,int e)
{
    this->n=n;
    this->e=e;
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
              this->edges[i][j]=a[i][j];
        }
     }
}

输出图

void DispMatGraph()
{
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            if(edge[i][j]==INF)
                 printf("%4s","∞");
            else
                 printf("%4d",edges[i][j]);     
           printf("\n");
         }
     }
}

邻接表

在含n个顶点的图G的邻接表中，顶点i（0≤i≤n-1）的每一条出边<i，j>（权值为W）对应一个边结点，顶点i的所有出边的边结点构成一个单链表，其中边结点的类型ArcNode
定义如下

struct ArcNode        //边结点类型
{
    int adjvex;        //邻接点
    int weight;        //权值
    ArcNode* nextarc； //指向下一边的边结点
};

给顶点i的单链表加上一个头结点，包含顶点i的信息和指向第一条边的边结点的指针，头结点的类型如下

struct HNode            //头结点类型
{
    string info;        //顶点信息
    ArcNode* firstarc;  //指向第一条边的边结点
};

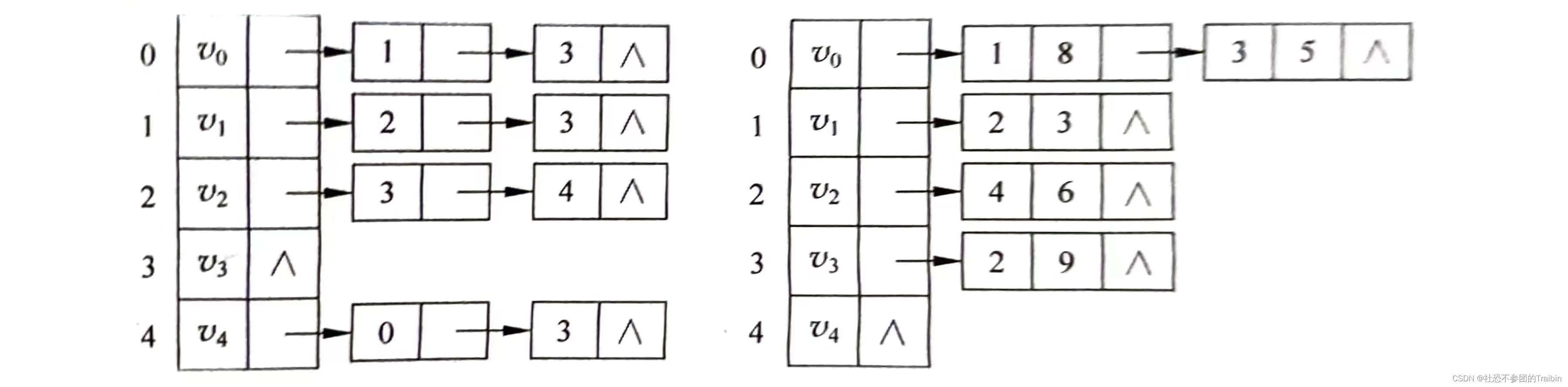图3：有向图的邻接表和有向图包含权值的邻接表

设计图的邻接表类AdjGraph如下

template<class i>
class AdjGraph		//图邻接表类
{
public:
	HNode adjlist[MAXV];	//头结点数组
	int n, e;
	AdjGraph()
	{
		for (int i = 0; i < MAXV; i++)
		{
			adjlist[i].firstarc = NULL;
		}
	}
	~AdjGraph()
	{
		ArcNode* pre, * p;
		for (int i = 0; i < n; i++)		//遍历所有头结点
		{
			pre = adjlist[i].firstarc;	//用一个ArcNode指针指向头结点的fitst区域
			if (pre != NULL)			//若不为空
			{
				p = pre->nextarc;		//则用另外一个ArcNode指针指向头结点的下一个结点
				while (p != NULL)		//释放过程，循环删除
				{
					delete pre;			
					pre = p; p = p->nextarc;	//两个指针同步后移
				}
				delete pre;
			}
		}
	}
	void CreateAdjGraph(int a[][MAXV], int n, int e);	//通过a，n，e来建立图的邻接表	
	void DispAdjGraph();								//输出图的邻接表
	int Degree1(AdjGraph* G, int v);					//计算无向图某个顶点的度，v为顶点名称
	i Degree2(AdjGraph& G, int v);				//计算有向图某个顶点的出度和入度，v为顶点名称
};

图的基本运算在邻接表中的实现

假设给定邻接矩阵数组啊，顶点数n和边数e来建立图的。

邻接表存储结构

template<typename i>
void AdjGraph<i>::CreateAdjGraph(int a[][MAXV], int n, int e)
{
	ArcNode* p;
	this->n = n; this->e = e;
	for (int i = 0; i < n; i++)
	{
		for (int j = n - 1; j >= 0; j--)
		{
			if (a[i][j] != 0 && a[i][j] != INF)
			{
				p = new ArcNode;					//指针类型的构造函数
				p->adjvex = j;
				p->weight = a[i][j];
				p->nextarc = adjlist[i].firstarc;	//采用头插法插入p
				adjlist[i].firstarc = p;

			}
		}
	}
}

输出图邻接表

template<typename i>
void AdjGraph<i>::DispAdjGraph()
{
	ArcNode* p;
	for (int i = 0; i < n; i++)						//遍历每一个头结点
	{
		printf(" [%d]", i);
		p = adjlist[i].firstarc;					//p指向第一个邻接点
		if (p != NULL)
			printf("->");
		while (p!= NULL)
		{
			printf("(%d,%d)", p->adjvex, p->weight);
			p = p->nextarc;							//p移向下一个邻接点
		}
		printf("\n");
	}
}

邻接表计算无向图某个顶点的度

template<typename i>
int AdjGraph<i>::Degree1(AdjGraph* G, int v)			//主要是用来统计某个顶点v的边数的算法
{
	int d = 0;
	ArcNode* p = G->adjlist[v].firstarc;
	while (p != NULL)								//对顶点v中的边数进行统计
	{
		d++;
		p = p->nextarc;
	}
	return d;
}

邻接表计算有向图某个顶点的出度和入度

template<typename i>
i AdjGraph<i>::Degree2(AdjGraph& G, int v)
{
	i ans = { 0,0 };						//ans[o]累计出度，ans[i]累计入读
	ArcNode* p = G.adjlist[v].firstarc;
	while (p != NULL)						//统计单链表v中顶点边结点个数
	{
		ans[0]++;
		p = p->nextarc;
	}
	for (int i = 0; i < G.n; i++)			//统计所有adjvex为v的边结点个数即为顶点v的入读
	{
		p = G.adjlist[i].firstarc;
		while (p != NULL)
		{
			if (p->adjvex == v)
			{
				ans[1]++;
				break;						//在一个单链表中最多只有一个这样的结点
			}
			p = p->nextarc;
		}
	}
	return ans;								//返回出度和入读
}

图的遍历

从给定图中任意指定的顶点（称为初始点）出发，按照某种搜索方法沿着图的边访问图中的所有顶点，使每个顶点访问一次且仅访问一次，这个过程称为图的遍历。图的遍历得到的顶点序列称为图遍历序列。

抽象操作，可以是对结点进行的各种处理，这里简化为输出结点的数据信息。
为了保证图中的各顶点在遍历过程中访问到且仅访问一次，需要为每个顶点设一个访问标志；
可以为图设置一个访问标志数组visited［n］，用于标示图中每个顶点是否被访问过，它的所有数组元素初始值为0，表示顶点均未被访问，一旦访问过顶点vi，则置访问标志数组中的visited［i］为1，以表示该顶点已访问。

深度优先遍历

思想（先深搜索）：
1、深度优先遍历是指在图中任选一个顶点V，访问V并以V作为初始点；
2、选择一个与顶点V相邻且未曾访问过的顶点W，访问W，并以W作为新的出发点，继续进行深度优先遍历；
3、若访问到某个顶点时，发现该顶点的所有邻接点均已访问过，则回溯到前一个访问过的顶点，从该顶点出发继续进行深度优先遍历。直到一直回溯到出发顶点V，并且图中与顶点V邻接的所有顶点均被访问过。
4、若此时图中任有未访问的顶点（说明是非连通图），则另选一个尚未访问的顶点作为新的出发点，重复上述过程，直到图中所有顶点均已被访问为止。

基本定义的结构体和类如下

#include<iostream>
#include<string>
using namespace std;
const int INF = 0x3f3f3f3f;
const int MAXV = 1000;
struct ArcNode
{
	int adjvex;		//邻接点
	int weight;		//权值
	ArcNode* nextarc;	//指向下一条边的边结点
};
struct HNode
{
	string info;	//顶点信息
	ArcNode* firstarc;	//指向第一条边的边结点
};

class AdjGraph		//图邻接表类
{
public:
	HNode adjlist[MAXV];	//头结点数组
	int n, e;
	AdjGraph()
	{
		for (int i = 0; i < MAXV; i++)
		{
			adjlist[i].firstarc = NULL;
		}
	}
	~AdjGraph()
	{
		ArcNode* pre, * p;
		for (int i = 0; i < n; i++)		//遍历所有头结点
		{
			pre = adjlist[i].firstarc;	//用一个ArcNode指针指向头结点的fitst区域
			if (pre != NULL)			//若不为空
			{
				p = pre->nextarc;		//则用另外一个ArcNode指针指向头结点的下一个结点
				while (p != NULL)		//释放过程，循环删除
				{
					delete pre;
					pre = p; p = p->nextarc;	//两个指针同步后移
				}
				delete pre;
			}
		}
	}
	void DFS(AdjGraph& G, int v);		//深度优先遍历（邻接表）
    void BFS(AdjGraph& G, int v);		//广度优先遍历（邻接表）
};

深度优先遍历算法（邻接表）

int visited[MAXV];						//全局标志数组，分辨顶点是否访问
void AdjGraph::DFS(AdjGraph& G, int v)
{
	cout << v << " ";							//输出访问的顶点
	visited[v] = 1;								//将访问的顶点置1
	ArcNode* p = G.adjlist[v].firstarc;			//将p指向顶点v的第一个邻接点
	while (p != NULL)
	{
		int w = p->adjvex;						//邻接点为w
		if (visited[w] == 0)					//若w顶点未被访问，递归访问
		{
			DFS(G, w);
		}
		p = p->nextarc;							//将p置为下一个邻接点
	}
}

深度优先遍历算法（邻接矩阵）

邻接矩阵结构类型代码见上——邻接矩阵的基本结构运行算法代码

该代码是类内声明类外定义

int visited[MAXV];
void MaxGraph::DFS(MaxGraph& g, int v)
{
    cout << v << "  ";                  //访问顶点v
    visited[v] = 1;                     //置顶点v为1，表示已经访问
    for (int w = 0; w < g.n; w++)
    {
        if (g.edges[v][w] != 0 && g.edges[v][w] != INF)
        {
            if (visited[w] == 0)           //存在边<v，w>并且w没有被访问
            {
                DFS(g, w);                  //若w顶点没有被访问，递归访问它
            }
        }        
    }
}

广度优先遍历

广度优先遍历算法（邻接表）

void AdjGraph::BFS(AdjGraph& G, int v)
{
	ArcNode* p;  int  queue[MAXV], first = 0, last = 0;//定义循环队列并初始化first=0,last=0，first指针指向队头元素的前一个位置，last指向队尾元素
	int w;
	cout << G.adjlist[v].info<< " ";  //  访问v
	visited[v] = 1;
	//v进队
	last = (last + 1) % MAXV;
	queue[last] = v;
	while (first != last)//若循环队列不为空
	{
		first = (first + 1) % MAXV;
		w = queue[first];//出队并赋值给w
		p = G.adjlist[w].firstarc;//找到与顶点w邻接的第一个顶点
		while (p != NULL)//当p=NULL时，表示顶点的所有邻接点都被访问过，继续判断循环队列是否为空
		{
			if (visited[p->adjvex] == 0)//如果当前邻接顶点未被访问
			{
				cout << G.adjlist[p->adjvex].info << " ";  //  访问相邻顶点
				visited[p->adjvex] = 1;//  置该顶点已被访问
				last = (last + 1) % MAXV;// 该顶点进队
				queue[last] = p->adjvex;
			}
			p = p->nextarc;  //查看下一个邻接点
		}
	}
}

广度优先遍历算法（邻接矩阵）

该代码是类内声明类外定义

void MaxGraph::BFS(MaxGraph& g, int v)
{
    int visited[MAXV];
    memset(visited, 0, sizeof(visited));        //初始化visited数组
    queue<int>qu;                               //定义一个队列
    cout << v << " ";                           //访问顶点v
    visited[v] = 1;                             //置已访问标记
    qu.push(v);                                 //顶点v入队
    while (!qu.empty())
    {
        int u = qu.front(); qu.pop();           //出队顶点u
        for (int i = 0; i < g.n; i++)
        {
            if (g.edges[u][i] != 0 && g.edges[u][i] != INF)
            {
                if (visited[i] == 0)            //存在边<u,i>并且顶点i未被访问
                {
                    cout << i << " ";           //访问邻接点i
                    visited[i] = 1;             //置已访问标记
                    qu.push(i);                 //邻接点i入队
                }
            }
        }
    }
}

生成树和最小生成树

生成树：包含了图中全部顶点的一个极小连通子图，所有顶点连通但又不形成回路，至少要有n-1条边，才可以使得全部顶点连通
由生成树的定义，可以看出生成树具有以下特点：
1、n个顶点（全部顶点）2、是连通的 3、有n-1条边 4、无回路
避免：少——不连通多——构成回路，不满足极小　
最小生成树：在连通网(带权图)中，各边权值之和最小的生成树称为最小生成树

两种常用的构造最小生成树的算法：

Prim算法

#include <iostream>
using namespace std;
#define MAXVEX 6//定义顶点最大个数
#define INF 1000//定义无穷大为1000
typedef char vertexType;//顶点类型定义为字符型
struct Graph {
	vertexType vexs[MAXVEX];//存放顶点的一维数组
	int arc[MAXVEX][MAXVEX];//邻接矩阵，存放边
	int nVex, nEdge;//存放图中的顶点数和边数
};
void  Prim(Graph g, int v)//Prim算法从顶点v出发构造最小生成树
{
	int lowcost[MAXVEX];//lowcost数组，存储候选最短边的权值
	int min;
	int closest[MAXVEX];//closest数组，存储候选最短边,例如closest［i］=k，表示候选最短边(vi, vk)
	int i, j, k;

	for (i = 0; i < g.nVex; i++)	//给lowcost[]和closest[]置初值
	{
		lowcost[i] = g.arc[i][v];
		closest[i] = v;
	}
	lowcost[v] = 0;	//lowcost[v] = 0表示顶点v属于集合U
	for (i = 1; i <= g.nVex - 1; i++)	  	//输出(n-1)条最小生成树的边
	{
		min = INF;//给min初值
		for (j = 0; j < g.nVex; j++)//在lowcost中找最小值，即在候选边中找最短边
			if (lowcost[j] != 0 && lowcost[j] < min)
			{
				min = lowcost[j];
				k = j;			//记录最短边的下标
			}
		cout << " 边(" << closest[k] << "，" << k << ")权为:" << min;
		cout << "      即:边(" << g.vexs[closest[k]] << "，" << g.vexs[k] << ")权为:" << min << endl;
		lowcost[k] = 0;		//标记顶点k已经加入U
		for (j = 0; j < g.nVex; j++)  //新顶点k从集合V-U进入集合U后，修改更新数组lowcost和closest
			if (lowcost[j] != 0 && g.arc[j][k] < lowcost[j])
			{
				lowcost[j] = g.arc[j][k];
				closest[j] = k;
			}
	}
}
int main()
{
	Graph g;//定义结构体变量g，用于存储图
	g.nVex = 6;//存储顶点个数
	g.nEdge = 10;//存储边的个数
	int i, j;
	for (i = 0; i < g.nVex; i++)   //初始化邻接矩阵
		for (j = 0; j < g.nVex; j++)
		{
			g.arc[i][j] = INF;//边的权值初始化为无穷大
		}
	//存顶点
	g.vexs[0] = 'A'; g.vexs[1] = 'B'; g.vexs[2] = 'C';
	g.vexs[3] = 'D'; g.vexs[4] = 'E'; g.vexs[5] = 'F';
	//存边
	g.arc[0][1] = 6; g.arc[0][2] = 1; g.arc[0][3] = 5;
	g.arc[1][0] = 6; g.arc[1][2] = 5; g.arc[1][4] = 3;
	g.arc[2][0] = 1; g.arc[2][1] = 5; g.arc[2][3] = 5;
	g.arc[2][4] = 6; g.arc[2][5] = 4;
	g.arc[3][0] = 5; g.arc[3][2] = 5; g.arc[3][5] = 2;
	g.arc[4][1] = 3; g.arc[4][2] = 6; g.arc[4][5] = 6;
	g.arc[5][2] = 4; g.arc[5][3] = 2; g.arc[5][4] = 6;

	cout << " 最小生成树的边依次是：" << endl;
	Prim(g, 0);//从顶点0出发构造最小生成树

	return 0;
}

kruskal算法

最小生成树的初始状态为只有n个顶点而无边。此时，图中每个顶点自成一个连通分量。
然后，按照边的权值由小到大的顺序，考察G的边集E中的各条边。
若被考察的边的两个顶点属于T的两个不同的连通分量，则将此边作为最小生成树的边加入到T中，同时把两个连通分量连接为一个连通分量；
若被考察边的两个顶点属于同一个连通分量，则不能选择此边，以免造成回路，继续考察下一条边，如此下去，当T中的连通分量个数为1时，此连通分量便为G的一棵最小生成树。

#include <iostream>
using namespace std;
#define MAXUEX 6//定义顶点最大个数
#define INF 1000//定义无穷大为1000
typedef char vertexType;//顶点类型定义为字符型
struct Graph {
	vertexType vexs[MAXUEX];//顶点表，存放顶点的一维数组
	int arc[MAXUEX][MAXUEX];//邻接矩阵，存放边
	int nVex, nEdge;//存放图中的顶点数和边数
};
struct Edge
{
	int u;//边的起始顶点
	int v;//边的终止顶点
	int w;//边的权值
};

void InsertSort(Edge E[], int n)//插入排序，对E数组所存的边按权值递增排序
{
	int i, j;   //循环变量
	Edge temp;     //存储待排序元素
	for (i = 1; i < n; i++) {
		j = i;
		temp = E[i];                         //待排序元素赋值给临时变量
		while (j > 0 && temp.w < E[j - 1].w) {   //当未达到数组的第一个元素或者待插入元素小于当前元素
			E[j] = E[j - 1];             //就将该元素后移
			j--;          //下标减1，继续比较
		}
		E[j] = temp;                 //插入位置已经找到，立即插入
	}
}

void Kruskal(Graph g)
{
	int i, j, u1, v1, sn1, sn2, k;
	int vset[MAXUEX];//记录每个顶点所在的连通分量编号
	Edge E[10];//定义结构体数组E，用于存储边
	k = 0;	//E数组从下标0开始存储边
	for (i = 0; i < g.nVex; i++)	//将邻接矩阵arc[][]中的边存储到数组E
		for (j = 0; j <= i; j++)
			if (g.arc[i][j] != INF)
			{
				E[k].u = i;  E[k].v = j;  E[k].w = g.arc[i][j];
				k++;
			}
	InsertSort(E, g.nEdge);		//对E数组按边权值递增排序

	for (i = 0; i < g.nVex; i++) 	//初始化辅助数组，记录每个顶点的连通分量编号
		vset[i] = i;//每个顶点各自为一个连通分量

	k = 1;		//k表示当前构造生成树的第几条边,用于控制循环次数
	j = 0;		//从E数组中下标0处开始选边
	while (k <= g.nVex - 1)		//循环n-1次，生成最小生成树的n-1条边
	{
		u1 = E[j].u; v1 = E[j].v;	//取一条边的头尾顶点
		sn1 = vset[u1];
		sn2 = vset[v1];		//分别得到两个顶点所属的连通分量编号
		if (sn1 != sn2)  		//如果两顶点属于不同的连通分量，这条边可以选为最小生成树的边
		{
			cout << " 边(" << u1 << "，" << v1 << ")权为:" << E[j].w;
			cout << "      即:边(" << g.vexs[u1] << "，" << g.vexs[v1] << ")权为:" << E[j].w << endl;
			k++;		   	//最小生成树的边数增1
			for (i = 0; i < g.nVex; i++)  	//两个不同的连通分量统一编号
				if (vset[i] == sn2) 	//连通分量编号为sn2的顶点改为sn1
					vset[i] = sn1;
		}
		j++;			//找E数组中的下一条边
	}
}
int main()
{
	Graph g;//定义结构体变量g，用于存储图
	g.nVex = 6;//存储顶点个数
	g.nEdge = 10;//存储边的个数
	for (int i = 0; i < g.nVex; i++)   //初始化邻接矩阵
		for (int j = 0; j < g.nVex; j++)
		{
			g.arc[i][j] = INF;//边的权值初始化为无穷大
		}
	//存顶点
	g.vexs[0] = 'A'; g.vexs[1] = 'B'; g.vexs[2] = 'C';
	g.vexs[3] = 'D'; g.vexs[4] = 'E'; g.vexs[5] = 'F';
	//存边
	g.arc[0][1] = 6; g.arc[0][2] = 1; g.arc[0][3] = 5;
	g.arc[1][0] = 6; g.arc[1][2] = 5; g.arc[1][4] = 3;
	g.arc[2][0] = 1; g.arc[2][1] = 5; g.arc[2][3] = 5;
	g.arc[2][4] = 6; g.arc[2][5] = 4;
	g.arc[3][0] = 5; g.arc[3][2] = 5; g.arc[3][5] = 2;
	g.arc[4][1] = 3; g.arc[4][2] = 6; g.arc[4][5] = 6;
	g.arc[5][2] = 4; g.arc[5][3] = 2; g.arc[5][4] = 6;
	cout << " 最小生成树的边依次是：" << endl;
	Kruskal(g);
	system("pause");

	return 0;
}